Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\) \(\overrightarrow{IA}=2\overrightarrow{IB}-4\overrightarrow{IC}\)
\(\overrightarrow{IA}=2\overrightarrow{IB}-2\overrightarrow{IC}-2\overrightarrow{IC}=2\overrightarrow{CB}-2\overrightarrow{IC}\)
\(=2\left(\overrightarrow{AB}-\overrightarrow{AC}\right)-2\left(\overrightarrow{AC}-\overrightarrow{AI}\right)\)
\(\overrightarrow{IA}=2\overrightarrow{AB}-2\overrightarrow{AC}-2\overrightarrow{AC}+2\overrightarrow{AI}\)
\(\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}\)
\(b,\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}=\dfrac{4}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(1\right)\)
\(\overrightarrow{JG}=\overrightarrow{AG}-\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AM}-\dfrac{2}{3}\overrightarrow{AB}\)\((\) \(\) \(M\) \(trung\) \(điểm\) \(BC)\)
\(\overrightarrow{JG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}-\dfrac{2}{3}\overrightarrow{AB}=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=-\dfrac{1}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\overrightarrow{IJ}=-4\overrightarrow{JG}\Rightarrow I,J,G\) \(thẳng\) \(hàng\)

Gt ⇒ \(2\left|\overrightarrow{MC}+\overrightarrow{MA}+\overrightarrow{MB}\right|=3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Do G là trọng tâm của ΔABC
⇒ \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\)
⇒ VT = 6MG
I là trung điểm của BC
⇒ \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\)
⇒ VP = 6MI
Khi VT = VP thì MG = MI
Vậy tập hợp các điểm M thỏa mãn ycbt là đường trung trực của đoạn thẳng IG

\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
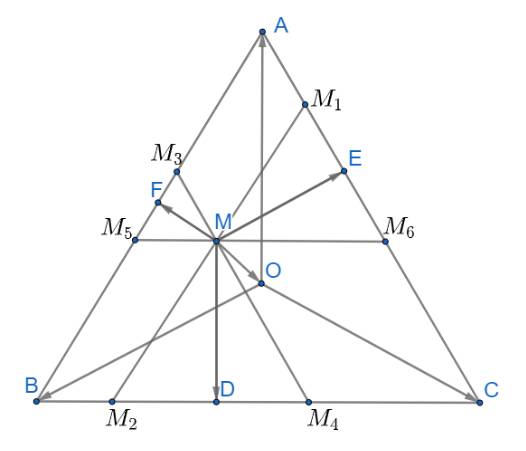

Có vẻ không đúng.
Giả sử \(\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow M\equiv B\) (Vô lí)