Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABK và ΔHCK có
KA=KH
góc AKB=góc HKC
KB=KC
Do đo: ΔABK=ΔHKC
b: \(BC=\sqrt{8^2+10^2}=2\sqrt{41}\)
\(AK=\dfrac{BC}{2}=\sqrt{41}\)
c: Ta co: ΔEAD vuông tại A
mà AI là đường trung tuyến
nên IA=IE
=>ΔIAE cân tại I
=>\(\widehat{IAE}=\widehat{IEA}\)

a: Xét ΔADM có
AB là đường cao
AB là đường trung tuyến
Do đo: ΔADM cân tại A
=>AD=AM và AB là tia phân giác của góc DAM(1)
Xét ΔADP có
AK là đường cao
AK là đường trung tuyến
DO đo: ΔADP cân tạiA
=>AD=AP và AC là phân giác của góc DAP(2)
Từ (1) và (2) suy ra AM=AD=AP
b: Từ (1) và (2) suy ra góc MAP=2x90=180 độ
=>M,A,P thẳng hàng
mà AM=AP
nên Alà trung điểm của MP

A B C D E I F Từ D vẽ đường thẳng song song với AC cắt BC tại F
Ta có: \(\bigtriangleup\)ABC cân tại A \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}\) (1)
DF//AC \(\Rightarrow\) DF//EC \(\Rightarrow\) \(\begin{cases} \widehat{ACB}=\widehat{DFB}(2)\\ \widehat{FDI}=\widehat{IEC}(3) \end{cases}\)
Từ (1);(2) \(\Rightarrow\) \(\widehat{ABC}=\widehat{DFB}\)
\(\Rightarrow\) \(\bigtriangleup\)DFB cân tại D
\(\Rightarrow\) BD=DF.
Mà BD=CE(gt) \(\Rightarrow\) CE=DF.
Xét \(\bigtriangleup\)FDI và \(\bigtriangleup\)CEI có:
DF=CE(cmt)
\(\widehat{FDI}=\widehat{IEC}\) (cmt)
DI=IE(I là trung điểm DE)
\(\Rightarrow\) \(\bigtriangleup\)FDI = \(\bigtriangleup\)CEI (c-g-c)
\(\Rightarrow\) \(\widehat{FID}=\widehat{EIC}\)
Ta có: \(\widehat{DIC}+\widehat{CIE}\) = 180o
Mà \(\widehat{FID}=\widehat{EIC}\) (cmt)
\(\Rightarrow\) \(\widehat{DIC}+\widehat{DIF}\) = 180o
\(\Rightarrow\) \(\widehat{FIC}=180^{0}\)
Hay \(\widehat{BIC}=180^{0}\)
\(\Rightarrow\) 3 điểm B,I,C thẳng hàng (đpcm)
Kẻ DH song song với AC (H thuộc BC)
Xét tam giác DBH. Ta có Góc BDH = góc BAC. B là góc chung => góc DHB = góc ACB. góc B = ACB (Tam giác ABC cân) => tam giác BDH cân lại D => DB = DH.
Xét 2 tam giác DHI và tam giác ECI
Ta có:
Góc HDI = góc IEC ( vị trí so le trong của DH và AC)
DH = CE ( cùng bằng DB)
DI = IE (gt)
=> 2 tam giác bằng nhau c.g.c
=> Góc DIB = Góc EIC
mà 2 góc này ở vị trí đối đỉnh => Thằng hàng.
(hoặc góc EIC + CID = 180 => DIB + CID = 180 độ => BIC là góc bẹt )

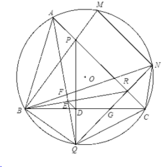
Ta có:
B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^

a: \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}-\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)

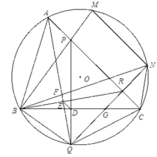
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q