Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

kẻ đường cao AH ( H ϵ BC)
trong tam giác vuông AHC:
\(\sin C\) = \(\dfrac{AH}{AC}\) ⇒ AH = AC.\(\sin C\) = 6\(\sin\left(30\right)\) = 3 cm
HC = \(\sqrt{AC^2-AH^2}\) = \(\sqrt{6^2-3^2}\) = 3\(\sqrt{3}\) cm
Trong tam giác vuông BHC:
BH = \(\sqrt{AB^2-AH^2}\) = \(\sqrt{5^2-3^2}\) = 4 cm
BC = HC + BH = 4 + 3\(\sqrt{3}\)

Ta có : \(BC^2=AB^2+AC^2\Leftrightarrow100=64+36\)(luôn đúng)
vậy tam giác ABC vuông tại A
tâm đường tròn nội tiếp tam giác ABC vuông tại A là trung điểm cạnh huyền
hay AI = IB = IC = BC/2 = 5

1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{6}=\dfrac{CD}{8}\)
mà BD+CD=10cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{CD}{8}=\dfrac{BD+CD}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{30}{7}cm;CD=\dfrac{40}{7}cm\)


Ta có AB : AC = 3 : 4 ⇔ A B 3 = A C 4 ⇒ A B 2 9 = A C 2 16
= A B 2 + A C 2 9 + 16 = A B 2 + A C 2 25 = B C 2 25 = 225 25 = 9
(Vì theo định lý Py-ta-go ta có A B 2 + A C 2 = B C 2 ⇔ A B 2 + A C 2 = 225 )
Nên A B 2 9 = 9 ⇒ AB = 9; A C 2 9 = 9 ⇒ AC = 12
Theo hệ thức lượng trong tam giác vuông ABC ta có:
A B 2 = B H . B C ⇒ B H = A B 2 B C = 81 15 = 5 , 4
Vậy BH = 5,4
Đáp án cần chọn là: A

Vì DE // AC Theo hệ quảTa lét ta có : \(\frac{DB}{AB}=\frac{DE}{AC}\Rightarrow\frac{AB-AD}{AB}=\frac{DE}{AC}\)
\(\Rightarrow\frac{AB-2}{AB}=\frac{2}{AC}\Rightarrow AB.AC-2AC=2AB\)
\(\Rightarrow AB.AC-2\left(AC+AB\right)=0\)(*)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\)(**)
Từ (*) ; (**) ta có hệ : \(\hept{\begin{cases}AB.AC-2\left(AC+AB\right)=0\\AB^2+AC^2=45\end{cases}}\)
bấm casio nhé, mode 9 _ 1 _ ấn hệ ra _ ''=''

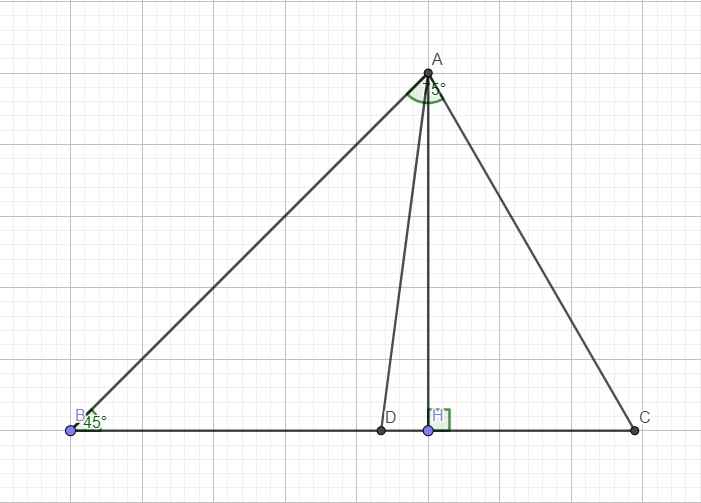
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=10.tan45^0=10\)
\(cosB=\dfrac{BH}{AB}\Rightarrow AB=\dfrac{BH}{cosB}=\dfrac{10}{cos45^0}=10\sqrt{2}\)
Do tam giác ABH vuông tại H \(\Rightarrow\widehat{BAH}=90^0-\widehat{B}=45^0\)
\(\Rightarrow\widehat{CAH}=\widehat{A}-\widehat{BAH}=75^0-45^0=30^0\)
Trong tam giác vuông ACH:
\(cos\widehat{CAH}=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{cos\widehat{CAH}}=\dfrac{10}{cos30^0}=\dfrac{20\sqrt{3}}{3}\)
AD là phân giác góc A \(\Rightarrow\widehat{CAD}=\dfrac{1}{2}\widehat{A}=\dfrac{75^0}{2}=37^030'\)
\(\Rightarrow\widehat{DAH}=\widehat{CAD}-\widehat{CAH}=37^030'-30^0=7^030'\)
Trong tam giác vuông ADH:
\(cos\widehat{DAH}=\dfrac{AH}{AD}\Rightarrow AD=\dfrac{AH}{cos\widehat{DAH}}=\dfrac{10}{cos\left(7^030'\right)}\approx10,1\)