Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

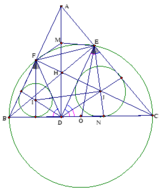
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
Tứ giác BFEC có B E C ^ = B F C ^ = 90 0
=> tứ giác BFEC nội tiếp đường tròn đường kính BC
Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF
∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^
∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)
=> ME=AH:2= MH do đó ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^
Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)
Nên O E B ^ + M E H ^ = 90 0 Suy ra M E O ^ = 90 0
⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^ = DFC ^
Tứ giác AFDC có A F C ^ = A D C ^ = 90 0 nên tứ giác AFDC nội tiếp đường tròn => B D F ^ = B A C ^
∆ BDF và ∆ BAC có B D F ^ = B A C ^ (cmt); B ^ chung do đó ∆ BDF ~ ∆ BAC(g-g)
Chứng minh tương tự ta có ∆ DEC ~ ∆ ABC(g-g)
Do đó ∆ DBF ~ ∆ DEC ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)
Vì ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác ⇒ D I D F = D J D C (2)
Từ (1) và (2) suy ra ∆ DIJ ~ ∆ DFC (c-g-c) => DIJ ^ = DFC ^


1) Chứng minh tứ giác AEHF nội tiếp đường tròn
BE là đường cao ∆ ABC ⇒ B E ⊥ A C ⇒ A E H ^ = 90 0
CF là đường cao ∆ ABC ⇒ C F ⊥ A B ⇒ A F H ^ = 90 0
Tứ giác AEHF có A E H ^ + A F H ^ = 180 0 nên tứ giác AEHF nội tiếp đường tròn
2) Chứng minh CE.CA = CD.CB
∆ ADC và ∆ BEC có
A D C ^ = B E C ^ = 90 0 (AD,BE là các đường cao)
C ^ chung
Do đó ∆ ADC ~ ∆ BEC(g-g)
⇒ D C E C = A C B C ⇒ D C . B C = C E . A C

a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{ABC}=180^0\)

a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: AH vuông góc với BC tại D
b:
Xét tứ giác CDFA có góc CDA=góc CFA=90 độ
nên CDFA là tứ giác nội tiếp
=>góc BFD=góc BCA
Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
=>góc AFE=góc ACB
Ta có: góc COE=180 độ-2 góc C
góc EFD=180 độ-góc AFE-góc BFD
=180 độ-2 góc C
=>góc COE=góc EFD
=>DOEF là tứ giác nội tiếp
