Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H thuộc BC). Biết AB=13cm,AH=12cm,HC=16cm. Tính AC,BC

Xét tam giác AHC có góc AHC=90
=>Tam giác AHC vuông tai H
Áp dụng định lí Py ta go cho tam giác AHC , ta có
AH^2+HC^2=AC^2
=>12^2+16^2=AC^2
=>400=AC^2
=>AC=20(cm)
Áp dụng định lí Py ta go cho tam giác AHB , ta có
AH^2+HB^2=AB^2
=>12^2+HB^2=13^2
=>HB^2=25
=>HB=5(cm)
Ta có BH+HC=BC
=>5+16=BC
=>BC=21 (cm)
Vậy AC=20cm ; BC=21cm

Ta có : AC^2=AH^2+HC^2 (định lí Pytago trong tam giác vuông ACH)
AC^2=12^2+16^2 AC^2=144+256 AC^2=400 AC=Căn 400=20(cm)
Ta có : AB^2=AH^2+HB^2 (định lí Pytago trong tam giác vuông ABH) 13^2=12^2+HB^2 169=144+HB^2 HB^2=169-144 HB^2=25
HB=Căn 25=5(cm) Ta có : BC=HB+HC BC=5+16 BC=21(cm)
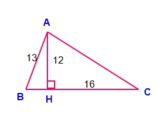
A B C H (Hình minh hoạ) AB = 13 cm, AH = 12 cm, HC = 16 cm
AH vuông góc với BC => Tam giác ABH và tam giác ACH vuông tại A
Áp dụng định lí Pi- ta - go trong tam giác AHC, có:
AC2 = AH2 + HC2
AC2 = 122 + 162 = 400 => AC = 20 cm
Áp dụng đinh lí Pi - ta -go trong tam giác ABH, có:
AB2 = AH2 + BH2
132 = 122 + BH2 => BH2 = 132 - 122 = 25 => BH = 5 cm
mà HC + BH = BC
16 + 5 = 21 = BC
Vậy AC = 20 cm, BC = 21 cm

Ta có : AC^2=AH^2+HC^2 (định lí Pytago trong tam giác vuông ACH) AC^2=12^2+16^2 AC^2=144+256 AC^2=400 AC=Căn 400=20(cm) Ta có : AB^2=AH^2+HB^2 (định lí Pytago trong tam giác vuông ABH) 13^2=12^2+HB^2 169=144+HB^2 HB^2=169-144 HB^2=25 HB=Căn 25=5(cm) Ta có : BC=HB+HC BC=5+16 BC=21(cm)
áp dụng pitago tính đc BH cộng đoạn thẳng tính đc BC,áp dụng pitago tính đc AC

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Ta có: BH+HC=BC(H nằm giữa B và C)
nên BC=16+16=32(cm)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+BC+AC=20+32+20=72\left(cm\right)\)
Lời giải:
Áp dụng định lý Pitago cho tam giác $AHC$ vuông tại $H$:
$HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
Áp dụng định lý Pitago cho tam giác $AHB$ vuông tại $H$:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20$ (cm)
Chu vi tam giác $ABC$:
$AB+BC+AC=AB+BH+CH+AC=20+16+16+20=72$ (cm)

Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25
⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)

Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)

hình tam giác đó trông thế nào vậy bạn
AC = 20 rồi không phải tính em ơi
xét tam giác AHC vuông tại H
=> AC^2 = HC^2 + AH^2
AC = 20 (gt); HC = 5 (gt)
=> 20^2 = 5^2 + AH^2
=> AH^2 = 400 - 25
=> AH^2= 375
=> AH = \(\sqrt{375}\) do AH > 0