Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)^A=1000 (quá đơn giản,bn tự lm)
b) Xét tam giác BAH=tam giác BDH (2cgv)
=>^BAH=^BDH (cặp góc t.ứ)
và tam giác CAH=tam giác CDH (2cgv)
=>^CAH=^CDH (cặp góc t.ứ)
Ta có:^BAC=^BAH+^CAH
^BDC=^BDH+^CDH
mà ^BAH=^BDH(cmt);^CAH=^CDH(cmt)
=>^BAC=^BDC
c)Vì ^ACB<^ABC (300<500)
=>AB<AC
mà HB là hình chiếu của đg xiên AB
HC là hình chiếu của đg xiên AC
=>HB<HC

a: góc B=90-30=60 độ
góc B>góc C
=>AC>AB
góc CAH=90-30=60 độ>góc C
=>CH>AH
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
CH chung
HA=HD
=>ΔCAH=ΔCDH
c: Xét ΔACB và ΔDCB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔACB=ΔDCB
=>góc CDB=góc CAB=90 độ

#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = ME (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB = CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{BHA}=\widehat{BHD}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`=> AB = BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD = CE`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`HA = HD (g``t)`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HM` chung
`=>` Tam giác `AMH =` Tam giác `DMH (c-g-c)`
`=> AM = DM (2` cạnh tương ứng `)`
Xét Tam giác `AMD` có: `AM = DM`
`->` Tam giác `AMD` là tam giác cân.

a: \(\widehat{C}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{C}< \widehat{B}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó: ΔAHC=ΔDHC
c: Xét ΔBAC và ΔBDC có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
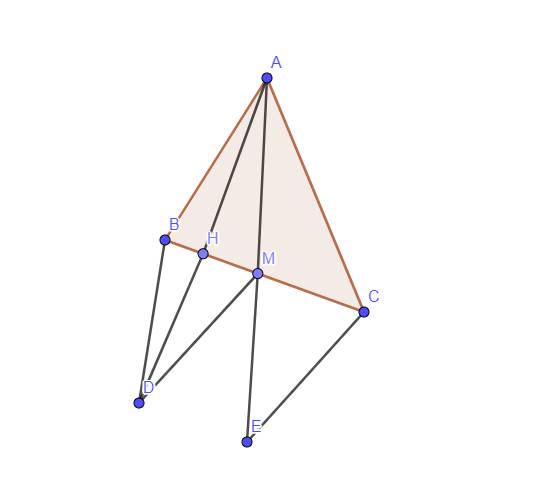
a: \(\widehat{A}=180^0-50^0-30^0=100^0\)
b: Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó:ΔBAD cân tại B
Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
Xét ΔBAC và ΔBDC có
BA=BD
AC=DC
BC chung
Do đó:ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}\)