BM
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DG
29 tháng 10 2020
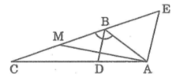
a) Từ A kẻ AE//BD cắt đường thẳng CB tại E
=> ^BAE=^DBA=^B/2=60* và ^ABE=60* (kề bù với ^B)
=> ∆ABE đều nên AB=BE=AE=6
Do BD//AE suy ra: BD/AE=CB/CE
mà CE=CB+BE=12+6=18cm
ta có BD/6=12/18 suy ra BD=12.6/18=4 (cm)
b) Xét ∆ABM có AB=BM =6cm (do BM=MC=BC/2)
nên ∆ABM cân tại B mà BD là đường phân giác nên cũng là đường cao
do đó BD vuông góc với AM.
10 tháng 8 2016
Đùng hệ thức lượng trong tam giác tính ra BC dùng tính chất đường phân giác tính ra BA dùng tiếp hệ thức lượng tính ra BD
Câu b/ đễ thấy tam giác ABM là tam giác cân tại B có BD là phân giác nên BD cũng là đường cao vậy BD vuông góc với AM
NT
7 tháng 8 2018
Hãy tích cho tui đi
vì câu này dễ mặc dù tui ko biết làm
Yên tâm khi bạn tích cho tui
Tui sẽ ko tích lại bạn đâu
THANKS
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{4^2+6^2}=2\sqrt{13}$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{4.6}{2\sqrt{13}}=\frac{12\sqrt{13}}{13}$ (cm)
b. Vì tam giác $ABC$ vuông tại $A$ nên $AM=\frac{BC}{2}=\sqrt{13}$ (cm)
CM
6 tháng 10 2017
Từ (1) và (2) suy ra: BM = AB ⇒ ∆ ABM cân tại B
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD ⊥ AM
AA
17 tháng 9 2018
a) Ta có:
ˆABD=ˆCBD=\(\frac{\widehat{ABC}}{2}\)=120∘: 2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘(so le trong)
ˆCBD=ˆAEB=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
\(\frac{BC}{CE}\)=\(\frac{DC}{AE}\)⇒BD=\(\frac{BC.AE}{CE}\)=\(\frac{12.6}{18}\)=4(cm)
b) Ta có:
MB=MC=\(\frac{1}{2}\).BC=\(\frac{1}{2}\).12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
tk mik nha
31 tháng 7 2020
a) Ta có:
\(\widehat{ABD}=\widehat{CBD}=\frac{\widehat{ABC}}{2}=\frac{120^o}{2}=60^o\)
Từ A kẻ đường thẳng song song với BD cắt CB tại E
Lại có:
\(\widehat{BAE}=\widehat{ABD}=60^o\) ( so le trong )
\(\widehat{CBD}=\widehat{AEB}=60^o\) ( đồng vị )
Suy ra tam giác ABE đều
=> AB = BE = EA = 6 ( cm ) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 ( cm )
Tam giác ACE có AE // BD nên suy ra :
\(\frac{BC}{CE}=\frac{BD}{AE}\)
\(\Rightarrow BD=\frac{BC.AE}{CE}=\frac{12.6}{18}=4\left(cm\right)\)
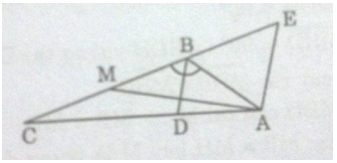
b) Ta có:
\(MB=MC=\frac{1}{2}.BC=\frac{1}{2}.12=6\left(cm\right)\left(2\right)\)
Từ (1) và (2) suy ra:
BM = AB => Tam giác ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao ( tính chất tam giác cân )
Vậy \(BD\perp AM\)