Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Sửa đề: Chứng minh DE\(\perp\)BC
Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
b: Sửa đề: F là giao điểm của AB và DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>AF=EC

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: ΔABD=ΔEBD
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
Xét ΔDAF và ΔDEC có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DF=DC
Do đó: ΔDAF=ΔDEC
=>AF=CE
c: Ta có: ΔDAF=ΔDEC
=>\(\widehat{DAF}=\widehat{DEC}\)
mà \(\widehat{DEC}=90^0\)
nên \(\widehat{DAF}=90^0\)
Ta có: \(\widehat{BAD}+\widehat{DAF}=\widehat{BAF}\)
=>\(\widehat{BAF}=90^0+90^0=180^0\)
=>B,A,F thẳng hàng
Xét ΔBFC có BA/AF=BE/EC
nên AE//FC

HÌNH KO CHUẨN LẮM
a) Xét \(\Delta ABD-\Delta EBD\) có :
BA = BE
\(\widehat{ABD}=\widehat{EBD}\)( phân giác )
DB là cạnh chung
=> \(\Delta ABD=\Delta EBD\)(C,G,C)
b) theo câu a) 2 tam giác ... = nhau
=> DA = DE ( 2 cạnh tương ứng )
c) theo câu a) 2 tam giác ... = nhau
=> \(\widehat{BAD}=\widehat{BED}=90^o\)( 2 góc tương ứng )
d) xét 2 tam giác \(\Delta EDB-\Delta EDC\)CÓ:
BED = CED ( góc vuông )
DE là cạnh chung
Để 2 tam giác \(\Delta EDB=\Delta EDC\) thì
\(\widehat{EBD}=\widehat{C}\)
MÀ \(\widehat{EBD}=\frac{1}{2}B\)
vậy để 2 tam giác đó = nhau thì góc B phải gấp 2 lần góc C

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD

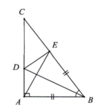
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE(ΔBAD=ΔBED)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>AF=CE
c: Ta có: ΔDAF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(1)
ta có: IF=IC
=>I nằm trên đường trung trực của CF(2)
ta có: BA+AF=BF
BE+EC=BC
mà BA=BE và AF=EC
nên BF=BC
=>B nằm trên đường trung trực của CF(3)
Từ (1),(2),(3) suy ra B,D,I thẳng hàng