Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

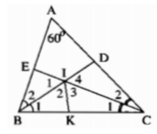
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
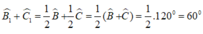
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID

Tia phân giác của góc BIC cắt BC ở K. \(\Delta ABC\) có \(\widehat{A}=60^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^0-60^0=120^0,\widehat{B_1}+\widehat{C_1}=\dfrac{\widehat{B}+\widehat{C}}{2}=\dfrac{120^0}{2}=60^0.\)
\(\Delta BIC\) có \(\widehat{B_1}+\widehat{C_1}=60^0\Rightarrow\widehat{BIC}=180^0-60^0=120^0.\)
Suy ra \(\widehat{I_1}=60^0,\widehat{I_4}=60^0.\)
IK là tia phân giác của góc BIC nên \(\widehat{I_2}=\widehat{I_3}=60^0.\)
\(\Delta BIE = \Delta BIK\) (g.c.g) => IE = IK (2 cạnh tương ứng).
\(\Delta CID = \Delta CIK\)(g.c.g) => ID = IK (2 cạnh tương ứng).
Do đó ID = IE.

a: Xét ΔABC có
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-60^0=120^0\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=60^0\)
\(\Leftrightarrow\widehat{BIC}=120^0\)

Em tham khảo tại link này nhé.
Câu hỏi của Tan Dang - Toán lớp 7 - Học toán với OnlineMath
a, Trong tam giác ABC có : góc ABC + góc ACB + góc BAC = 180 độ
=> góc ABC + góc ACB =180 độ - góc BAC = 180 độ - 60 độ = 120 độ
Mà BD và CE lần lượt là phân giác của góc ABC ; ACB nên
120 độ = 2.góc IBC + 2.góc ICB = 2.(góc IBC + góc ICB)
=> góc IBC + góc ICB = 120 độ : 2 = 60 độ
Trong tam giác IBC có : góc IBC + góc ICB + góc BIC = 180 độ
=> góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

Giải:
Kẻ IF là tia phân giác của \(\widehat{BIC}\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) ( 3 góc của \(\Delta ABC\) )
\(\Rightarrow\widehat{B}+\widehat{C}=120^o\) ( do \(\widehat{A}=60^o\) )
\(\Rightarrow\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)=\frac{1}{2}.120^o\)
\(\Rightarrow\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{C}=60^o\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=60^o\)
Trong \(\Delta BIC\) có: \(\widehat{BIC}+\widehat{B_1}+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{BIC}+60^o=180^o\)
\(\Rightarrow\widehat{BIC}=120^o\)
Vì IF là tia phân giác của \(\widehat{BIC}\) nên:
\(\widehat{I_2}=\widehat{I_3}=\frac{1}{2}\widehat{BIC}=60^o\)
Góc ngoài: \(\widehat{I_4}=\widehat{B_1}+\widehat{C_1}=60^o\)
\(\widehat{I_1}=\widehat{B_1}+\widehat{C_1}=60^o\)
Xét \(\Delta EIB,\Delta FIB\) có:
\(\widehat{I_1}=\widehat{I_2}\left(=60^o\right)\)
\(IB\): cạnh chung
\(\widehat{B_1}=\widehat{B_2}\left(=\frac{1}{2}\widehat{B}\right)\)
\(\Rightarrow\Delta EIB=\Delta FIB\left(g-c-g\right)\)
\(\Rightarrow IE=IF\) ( cạnh t/ứng ) (1)
Xét \(\Delta DIC,\Delta FIC\) có:
\(\widehat{I_3}=\widehat{I_4}\left(=60^o\right)\)
\(IC\): cạnh chung
\(\widehat{C_1}=\widehat{C_2}\left(=\frac{1}{2}\widehat{C}\right)\)
\(\Rightarrow\Delta DIC=\Delta FIC\left(g-c-g\right)\)
\(\Rightarrow ID=IF\) ( cạnh t/ứng ) (2)
Từ (1) và (2) suy ra \(ID=IE\)
\(\Rightarrowđpcm\)
Bài này có bạn khác giải rồi nhé