Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xet tram giac ABC , co :
A+B+C=180 độ
40+B+C=180 do
B+C=180-40=140 độ
Ma : ^AHB=HBC=ABC/2(HB la tia ohan giac goc B (gt))
ACH=BCH=ABC/2(HC la tia phan giac goc C(gt))
=>HBC=BCH=ABC+ABC/2=140/2=70 độ
xet tam giac HBC có :
HBC+HCB+H=180
70+H=180
H=180-70
=>H=110
****

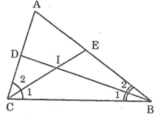
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o

a)gọi trung điểm của AB là H, của BC là I.
xét \(\Delta\) HBD và \(\Delta\) HAD có:
HB=HA
góc BHD= góc AHD=90độ
HD(chung)
suy ra 2 tam giac tren = nhau(c.g.c)
suy ra góc B=góc DAH\(\Rightarrow\) \(\Delta\) ABD là tam giác cân
chứng minh tương tự vs 2 tam giác EAI và ECI(c.g.c)
suy ra góc EAI= góc ECI\(\Rightarrow\) tam giác ACE là tam giác cân
câu b đợi tí mh nghĩ đã
m bị điên à tk 'nhóc quậy phá' ??? Đường trung trực của AB và AC cắt nhau tại I r mak m còn gọi trung điểm của BC là I
