Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
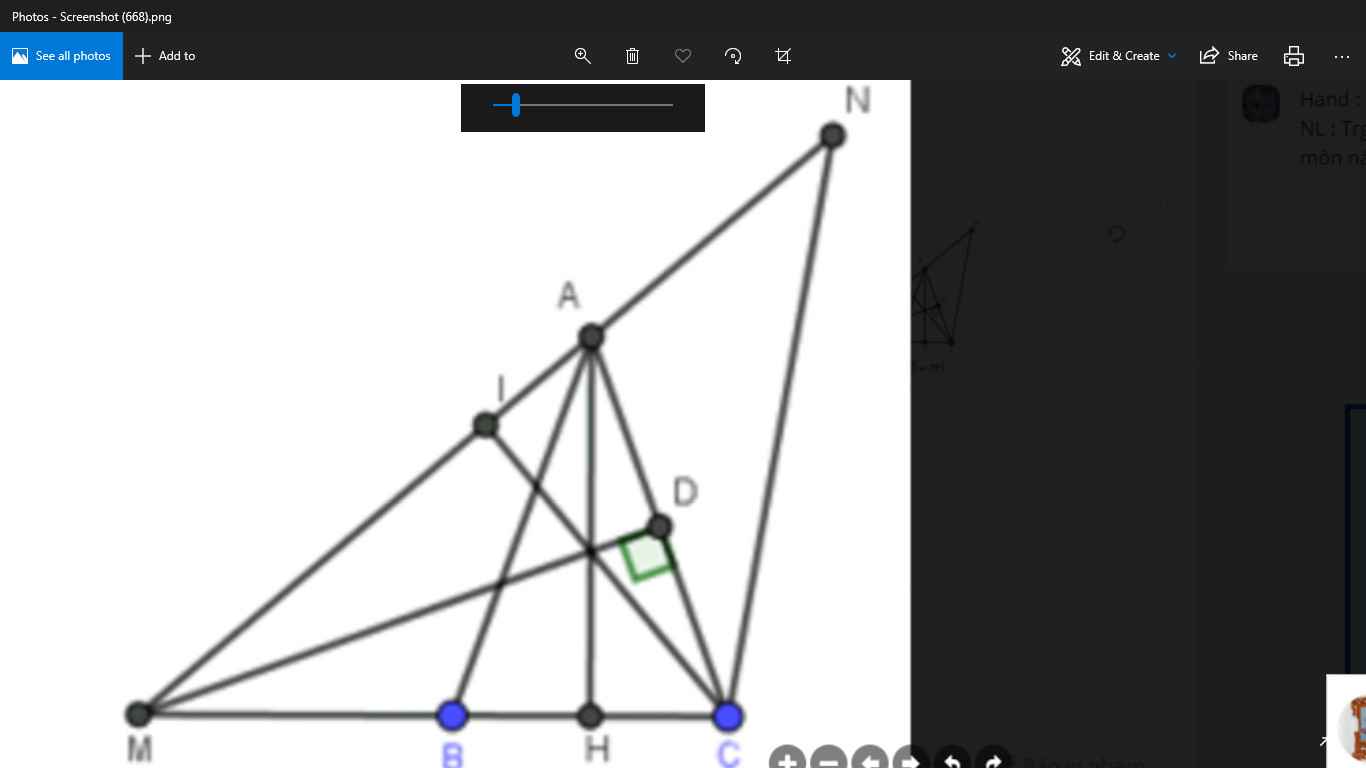
\(\text{a)}\Delta ABC\text{ cân tại }A\text{ có }\widehat{A}=40^0\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
\(\text{Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(BH=CH\text{(H là trung điểm BC)}\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{ÂHB}=\widehat{AHC}\)
\(\text{mà }\widehat{AHB}+\widehat{AHC}=180^0\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow AH\perp BC\)
\(\text{b)}\Delta AMC\text{ cân tại M}\text{ vì MD là đường trung trực}\)
\(\Rightarrow\widehat{MAD}=\widehat{MCD}=70^0\)
\(\text{Ta có:}\widehat{MAD}=\widehat{MAH}+\widehat{CAH}\)
\(\Rightarrow\widehat{MAH}=\widehat{MAD}-\widehat{CAH}=70^0-\dfrac{40^0}{2}=50^0\text{(vì AH là phân giác }\widehat{BAC}\text{)}\)
\(\text{c)Xét }\Delta ABM\text{ và }\Delta CAN\text{ có:}\)
\(BM=AN\text{(cách lấy điểm N)}\)
\(AB=AC\left(cmt\right)\)
\(\widehat{ABM}=\widehat{CAN}=180^0-70^0=110^0\)
\(\Rightarrow\Delta ABM=\Delta CAN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\text{(hai cạnh tương ứng)}\)
\(\text{d)Xét }\Delta MIC\text{ và }\Delta NIC\text{ có:}\)
\(IC\text{ cạnh chung}\)
\(\widehat{MIC}=\widehat{NIC}=90^0\)
\(\widehat{IMC}=\widehat{INC}\text{(vì }\Delta ABM=\Delta CAN\text{)}\)
\(\Rightarrow\Delta MIC=\Delta NIC\left(gn.cgv\right)\)
\(\Rightarrow MI=NI\)
\(\Rightarrow\text{I là trung điểm MN}\)

a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
c: Ta có: M nằm trên đường trung trực của AC
nên MA=MC
hay ΔMAC cân tại M

Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)
jfccfffcfffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ko đc đăng linh tinh