Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔABC có
BD,CE là trung tuyến
BD cắt CE tại G
=>G là trọng tâm
=>AG là trung tuyên của ΔABC
mà ΔABC cân tại A
nên AG là phân giác của góc BAC
b ΔACB cân tại A
mà AG là trung tuyến
nên AG là trung trực của BC
=>GB=GC
c: Xét ΔGAC có
CK,AI,GD là trung tuyến
=>CK,AI,GD đồng quy
=>CD,AI,BD đồng quy

a)Xét tam giác ABD và tam giác ACE,ta có:
A là góc chung
AB=AC(ví tam giác ABC cân tại A)
AE=AD(gt)
=> tam giác ABD=tam giác ACE(c.g.c)=>BD=CE( 2 cạnh tương ứng)
b)Vì BD,CE lần lượt là đường trung tuyến mà lại giao nhau tại G(mà BD=CE)=>GE=GD=1/3 BD=1/3 CE
=>EG=GD
Xét tam giác AEG và tam giác ADG ,ta có:
GE=GD(c/m trên)
AE=AD(gt)
AG cạnh chung
=>tam giác AEG=tam giác ADG(c.c.c)
=>góc EAG=góc DAG=>AG là tia p/g góc A
c)Ta có: Vì K là trung điểm AG;I là trung điểm GC và AD=DC
=>AI;CK:GD lần lượt là đường trung tuyến tam giác AGC=>BD;CK;AI đồng quy(t/c 3 đường trung tuyến của tam giác)

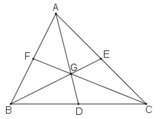
Trên đường trung tuyến AD có điểm G thỏa mãn: 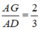
Suy ra: G là trọng tâm tam giác ABC.
Do tia BG cắt AC tại E nên E là trung điểm của AC.
Do tia CG cắt AB tại F nên F là trung điểm của AB.
Theo tính chất trọng tâm tam giác ta có:
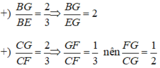
Chọn (B)

a) Do G là trọng tâm tam giác ABC nên AG = 2GM. Lại có AG = GD nên GD = 2GM hay GM = DM.
Xét tam giác DMB và tam giác GMC có:
DM = GM
BM = CM
\(\widehat{DMB}=\widehat{GMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta DMB=\Delta GMC\left(c-g-c\right)\)
\(\Rightarrow BD=CG\)
b) Do \(\Delta DMB=\Delta GMC\Rightarrow\widehat{FBM}=\widehat{ECM}\)
Xét tam giác FBM và tam giác ECM có:
\(\widehat{FMB}=\widehat{EMC}=90^o\)
BM = CM
\(\widehat{FBM}=\widehat{ECM}\)
\(\Rightarrow\Delta FBM=\Delta ECM\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BF=CE\left(đpcm\right)\)

Gọi I là trung điểm của BC, hiển nhiên A, I, G thẳng hàng ! AI là trung tuyến của tg ABC! Vì BD = CE nên CG=BG (=2/3 CE). Tạm giác BGC cân tại G, nên GI vuông góc với BC hay nói cách khác AI vuông góc BC : tạm giác ABC phải là tg cân tại A! Đpcm AG là phân giác góc A! 2/ EG=NG nên N là trung điểm CG( tính chất trung tuyến CG=2 GE)! Tương tự M là trung điểm AG! Vay thì GD , CM, AN là 3 trung tuyến của tam giác AGC, đồng quy! Mà GD cũng là BD!!!!
Chọn D