
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

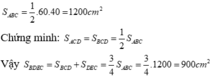


Dễ thấy \(S_{ABC}=\dfrac{40.60}{2}=1200\left(cm^2\right)\)
Lại có \(S_{BEC}=\dfrac{S_{ABC}}{2}\)(do chung đường cao hạ từ B xuống AC và \(CE=\dfrac{AC}{2}\))
Tương tự ⇒\(S_{BDE}=\dfrac{S_{ABE}}{2}=\dfrac{S_{ABC}}{4}\)
⇒\(S_{BDEC}=S_{BDE}+S_{BEC}=\dfrac{S_{ABC}}{4}+\dfrac{S_{ABC}}{2}=\dfrac{3S_{ABC}}{4}=\dfrac{3.1200}{4}=900\left(cm^2\right)\)

a/ Xét t/g ABC có D,E lần lượt là trung điểm AB ; AC
=> DE là đường trung bình t/g ABC
=> DE // BC ; DE = BC/2
=> DE // BF ; DE = BF(do F là trung điểm BC)
=> Tứ giác BDEF là hình bình hành
b/ Có BDEF là hbh
=> EF = BD
Xét t/g ABK vuông tại K có KD là đường trung tuyến
=> KD = 1/2 AB = BD=> EF = KD
Mà DE // BC
=> DE // KF
=> Tứ giác DEFK là htc
c/ Xét t/g AHC có ME là đường trung binh
=> ME = 1/2 HC ; ME // HC (1)
Xét t/g BHC có NF là đường trung bình
=> NF = 1/2 HC ; NF // HC (2)
(1) ; (2)
=> ME = NF ; ME // NF (3)
Xét t/g ABH có MN là đường trung bình
=> MN // AB ; MN = 1/2 ABMà
HC ⊥ AB
NF // HC=> MN ⊥ NF (4)(3) ; (4)
=> MNFE là hcn
=> NE = MF ; NE, MF cắt nhau tại trung điểm mỗi đoạn
CMTT ta có đpcm

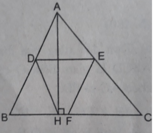
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2

a: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{1}{2}BC\)
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
b: Xét ΔABC có
D,F lần lượt là trung điểm của BA,BC
=>DF là đường trung bình của ΔABC
=>DF//AC và \(DF=\dfrac{AC}{2}\)
DF//AC
E\(\in\)AC
Do đó: DF//AE
Ta có: \(DF=\dfrac{AC}{2}\)
\(AE=\dfrac{AC}{2}\)
Do đó: DF=AE
Xét tứ giác ADFE có
DF//AE
DF=AE
Do đó: ADFE là hình bình hành
Xét tứ giác AFBI có
D là trung điểm chung của AB và FI
=>AFBI là hình bình hành