Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác IBC có: góc BIC + góc IBC + góc ICB = 180 độ ( định lý tổng 3 góc trong tam giác )
Mà góc BIC = 120 độ ( giả thiết ) => góc IBC + góc ICB = 180 độ - 120 độ = 60 độ
Vì BI là phân giác góc ABC ( giả thiết ) => góc IBC = \(\frac{1}{2}\)góc ABC
Vì CI là phân giác góc ACB ( giả thiết ) => góc ICB = \(\frac{1}{2}\)góc ACB
=>góc IBC + góc ICB = \(\frac{1}{2}\)góc ABC + \(\frac{1}{2}\)góc ACB = 60 độ
=> \(\frac{1}{2}\)( góc ABC + góc ACB ) = 60 độ
=> góc ABC + góc ACB = 120 độ
Xét tam giác ABC có: góc A + góc ABC + góc ACB = 180 độ ( định lý tổng 3 góc trong tam giác )
=> góc A + 120 độ = 180 độ
=> góc A = 60 độ

Cậu tự vẽ hình !
Theo tổng ba goác trong một tam giác , ta có :
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(70^0+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{ABC}+\widehat{ACB}=110^0\)
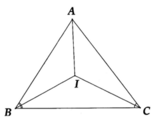
Vì I là là giao điểm ba đường phân giác nên
BI là phân giác của góc ABC
\(\Rightarrow\widehat{ABI}=\widehat{IBC}=\frac{\widehat{ABC}}{2}\)
CI là phân giác của góc ACB
\(\Rightarrow\widehat{ACI}=\widehat{ICB}=\frac{\widehat{ACB}}{2}\)
Ta có :
\(\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{100^0}{2}=50^0\)
Và áp dụng tổng 3 góc trong tam giác lên tam giác BIC thì
=> Góc BIC = 1800 - 500 = 1300

Bạn xem ở đường link này:
Câu hỏi của Cùng học toán đi - Toán lớp 6 - Học toán với OnlineMath

Hình vẽ a chèn không rõ được không, chắc giống của e thôi.
https://1drv.ms/u/s!AhUPZHs4UJtKilHrVZWqF8i6a584?e=0TIfMP
Ta có : \(\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BIC}=180^0-\frac{\widehat{ABC}}{2}-\frac{\widehat{ACB}}{2}\)( Do IB,IC là tia phân giác của góc ABC và ACB)
còn \(\widehat{BKC}=180^0-\widehat{KBC}-\widehat{KCB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BKC}=180^0-\frac{\widehat{xBC}}{2}-\frac{\widehat{yCB}}{2}\)( Do KB,KC là tia phân giác của góc ABC và ACB)
Mà \(\hept{\begin{cases}\widehat{xBC}=180^0-\widehat{ABC}\\\widehat{yCB}=180^0-\widehat{ACB}\end{cases}}\)\(\Rightarrow\widehat{BKC}=180^0-\left(\frac{180^0-\widehat{ABC}}{2}+\frac{180^0-\widehat{ACB}}{2}\right)\)
\(\Rightarrow\widehat{BKC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}\)
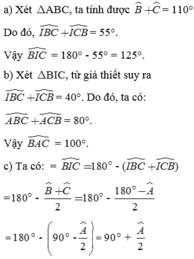
Ta có: góc C = 70 độ
=> góc BCI = 35 độ
=> góc IBC = 25
=> góc B = 50 độ
=> góc A = 60 độ
Vậy tam giác ABC có góc A = 60 độ; góc B = 50 độ; góc C = 70 độ
\(\frac{6}{7}\)