Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chú ý tam giác ABD cân tại B nên BM là đường phân giác cũng là đường cao, từ đó B M ⊥ A D .
b) Chú ý AK, BM, DH là ba đường cao của tam giác AMD.
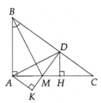

a) Xét tam giác \(AHD\) và tam giác \(AKD\):
\(\widehat{AHD}=\widehat{AKD}\left(=90^o\right)\)
\(AD\) cạnh chung
\(\widehat{HAD}=\widehat{KAD}\) (vì \(AD\) là tia phân giác góc \(A\) của tam giác \(ABC\))
Suy ra \(\Delta AHD=\Delta AKD\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\).
b) \(\Delta AHD=\Delta AKD\) suy ra \(DH=DK\) suy ra \(D\) thuộc đường trung trực của \(HK\).
\(AH=AK\) suy ra \(A\) thuộc đường trung trực của \(HK\)
suy ra \(AD\) là đường trung trực của \(HK\).
c) Xét tam giác \(AKE\) và tam giác \(AHF\):
\(\widehat{A}\) chung
\(AH=AK\)
\(\widehat{AHF}=\widehat{AKE}\left(=90^o\right)\)
suy ra \(\Delta AKE=\Delta AHF\) (g.c.g)
suy ra \(AE=AF\)
Xét tam giác \(AEF\) có: \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\) suy ra \(HK//EF\).
a: Trên tia BH có HB=HD
nên HB và HD là hai tia đối nhau
mà HB và HC là hai tia đối nhau
nên HD và HC là hai tia trùng nhau
=>\(D\in HC\)
b: Đề sai rồi bạn