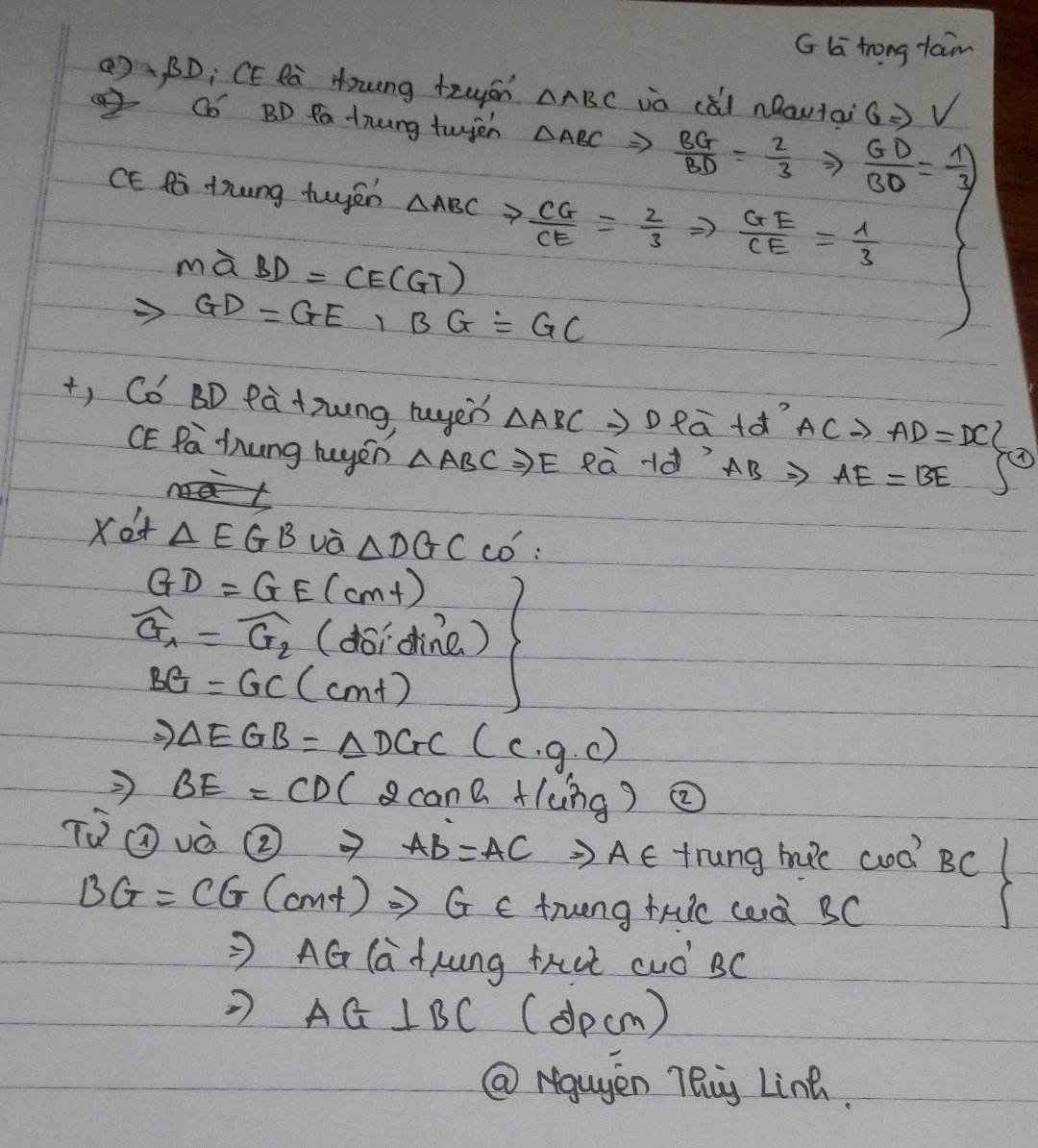Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

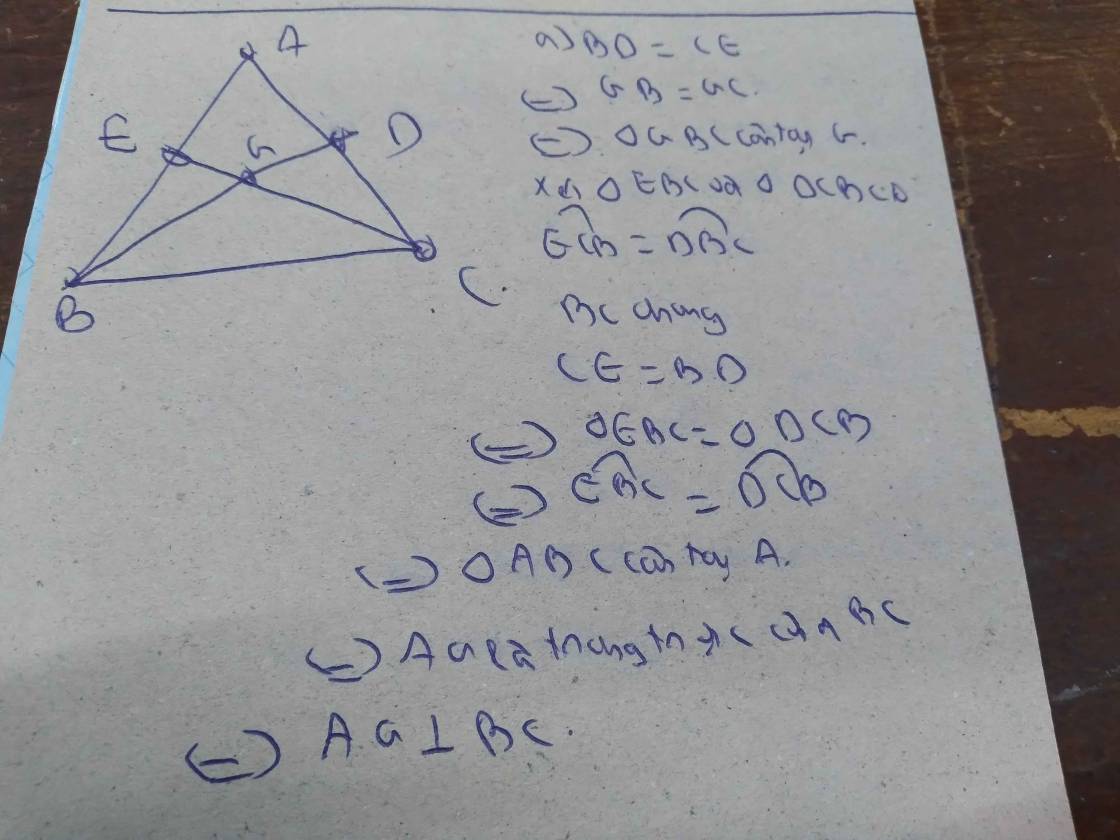
G là giao điểm của 2 đường trung tuyến BD và CE
Suy ra : G là trọng tâm tam giác ABC
Suy ra :
GD = 1/3 BD = 1/3 x 24 = 8 ( cm )
GE = 1/3 CE = 1/3 x 45 = 15 ( cm )
Xét tam giác ABC có :
E là trung điểm AB ( trung tuyến CE )
D là trung điểm AC ( trung tuyến BD )
Suy ra : ED là đường trung bình của tam giác ABC
Suy ra ED : = 1/2 x BC = 1/2 x 34 = 17 ( cm )
Vậy GD = 8 cm
GE = 15 cm
ED = 17 cm

Tự vẽ hình nhé !
Vì G là giao điểm 2 đường trung tuyến => G là trọng tâm
Xét Δ BDC có: \(\frac{GD}{BD}=\frac{1}{3}\) (vì \(\frac{GD}{BG}=\frac{2}{3}\) ) (T/c trọng tâm)
=> \(\frac{GD}{24}=\frac{1}{3}\) => GD = \(\frac{24.1}{3}\) = 8 (cm)
Tương tự, xét Δ EDC có: \(\frac{EG}{EC}=\frac{1}{3}\) (vì \(\frac{EG}{GC}=\frac{2}{3}\) ) (T/c trọng tâm)
=> \(\frac{EG}{45}=\frac{1}{3}\) => EG = \(\frac{45.1}{3}\) = 15 (cm)
Còn ED thì dựa vào t/c đường trung bình Δ ABC (AE=EB, AD=DC)

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC

1.gọi giao của BD và CE là O
ta có: OB=2/3 BD=> OB=2/3 x 9=6
ta có: OC=2/3 EC=> OC=2/3 x12=8
ta có:\(OC^2+OB^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
=> tam giác OBC vuông tại O=> BD_|_CE tại O
1.gọi giao của BD và CE là O
ta có: OB=2/3 BD=> OB=2/3 x 9=6
ta có: OC=2/3 EC=> OC=2/3 x12=8
ta có:$OC^2+OB^2=6^2+8^2=36+64=100$OC2+OB2=62+82=36+64=100
$BC^2=10^2=100$BC2=102=100
=> tam giác OBC vuông tại O=> BD_|_CE tại O

Ta có:
- BM = MN = NC = 2 cm.
- BD = BC/2 = 3 cm.
- CE = BC/2 = 3 cm.
Do đó, I là trung điểm của BD và K là trung điểm của CE.
Ta có:
- IK = ID/2 = 1,5 cm.
Vậy IK = 1,5 cm.