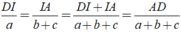Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

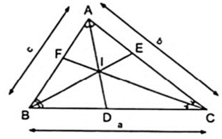
Chứng minh tương tự như câu a, ta được:
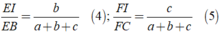
Công theo vế các đẳng thức ( 3 ),( 4 ),( 5 ) ta được:
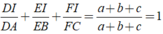

a, Xét \(\Delta ACF\) và \(\Delta ABE\) có:
\(\widehat{AFC}=\widehat{AEB}=90^0\)
\(\widehat{BAC}\) là góc chung
\(\Rightarrow\Delta ACF~\Delta ABE\left(g.g\right)\)
\(\Rightarrow\frac{AC}{AB}=\frac{AF}{AE}\)
\(\Rightarrow AC.AE=AB.AF\)
Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\widehat{CAB}\) là góc chung
\(\frac{AE}{AB}=\frac{AF}{AC}\)
\(\Rightarrow\Delta AEF~\Delta ABC\left(c.g.c\right)\)
b, Xét \(\Delta BDH\) và \(\Delta BEC\) có:
\(\widehat{EBC}\) là góc chung
\(\widehat{BEC}=\widehat{BDH}=90^0\)
\(\Rightarrow\Delta BDH~\Delta BEC\left(g.g\right)\)
\(\Rightarrow\frac{BH}{BC}=\frac{BD}{BE}\)
\(\Rightarrow BE.BH=BC.BD\left(1\right)\)
Tương tự như trên ta được: \(\Delta CDH~\Delta CFB\left(g.g\right)\)
\(\Rightarrow\frac{CH}{CB}=\frac{CD}{CF}\)
\(\Rightarrow CF.CH=CD.CB\left(2\right)\)
Từ (1) và (2) \(\Rightarrow BE.BH+CH.CF=BD.BC+BC.CD=BC\left(BD.CD\right)=BC^2\)
\(\Rightarrow BH.BE+CH.CF=BC^2\)
d,EI _|_ AB ; CE _|_ AB => EI // CE => AI/IF = AE/EC (đl)
EK _|_ AD; CD _|_ AD => EK // CD => AK/KD = AE/EC (đl)
=> AI/IF = AK/KD; xét tam giac AFD
=> IK // FD (1)
ER _|_ BC; AD _|_ BC => ER // AD => CR/RD = CE/EA (đl)
EQ _|_ CF; AF _|_ CF => AH // AF => CH/FH = CE/AE (đl)
=> CR/RD = CH/FH; xét tam giác CFD
=> HR // FD (2)
EK _|_ AD; AD _|_ BD => EK // BD => KH/HD = EH/HB (đl)
EH _|_ CF; CF _|_ BF => EH // FB => EH/HB = QH/HF (đl)
=> KH/HD = QH/HF
=> KH // ED (3)
(1)(2)(3) => I;K;H;R thẳng hàng (tiên đề Ơclit)

Sửa đề: ΔABC cân tại A
a:ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
=>AD vuông góc BC
b: Xét ΔAFI và ΔAEI có
AF=AE
góc FAI=góc EAI
AI chung
=>ΔAFI=ΔAEI
=>góc AFI=góc AEI
=>FI vuông góc AB
c: Xét ΔABC có
BE,AD là đường cao
BE cắt AD tại I
=>I là trực tâm
=>CI vuông góc AB
=>C,I,F thẳng hàng

Bài 10:
a) Xét ΔABE vuông tại E và ΔCBD vuông tại D có
\(\widehat{DBC}\) chung
Do đó: ΔABE\(\sim\)ΔCBD(g-g)
b) Xét ΔHDA vuông tại D và ΔHEC vuông tại E có
\(\widehat{AHD}=\widehat{CHE}\)(hai góc đối đỉnh)
Do đó: ΔHDA\(\sim\)ΔHEC(g-g)
Suy ra: \(\dfrac{HD}{HE}=\dfrac{HA}{HC}\)
hay \(HD\cdot HC=HE\cdot HA\)
Bài 11:
a) Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔABE\(\sim\)ΔACF(g-g)
b) Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔFHB\(\sim\)ΔEHC(g-g)
Suy ra: \(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
hay \(HE\cdot HB=HF\cdot HC\)
c) Ta có: ΔAEB\(\sim\)ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)
Áp dụng tính chất đường phân giác AD và BI và tam giác ABC và tam giác ABD.
Ta có: DI/IA = DB/AB = BD/c ( 1 )
Thay ( 2 ) vào ( 1 ) ta được: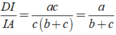
Suy ra: