Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó:MN là đường trung bình của ΔBAC
Suy ra: MN//BC
Xét ΔABH có
M là trung điểm của AB
MI//BH
Do đó:I là trung điểm của AH

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
Xét ΔABH có
M là trung điểm của AB
MI//BH
Do đó: I là trung điểm của AH

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành

a: Xét ΔABC có
E là trung điểm của AC
F là trung điểm của BC
Do đó: FE là đường trung bình
=>FE//DB và FE=DB
hay DEFB là hình bình hành

a) Sửa đề: MN cắt AH tại I
Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒MN//BC và \(MN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: MN//BC(cmt)
mà I∈MN(gt)
và H∈BC(gt)
nên IN//HC
Xét ΔAHC có
N là trung điểm của AC(gt)
IN//HC(cmt)
Do đó: I là trung điểm của AH(Định lí 1 về đường trung bình của tam giác)
b)
Ta có: Q đối xứng với P qua N(gt)
nên N là trung điểm của QP
Xét ΔABC có
P là trung điểm của BC(gt)
N là trung điểm của AC(gt)
Do đó: PN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒PN//AB và \(PN=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà Q∈PN và \(PN=\dfrac{PQ}{2}\)(N là trung điểm của PQ)
nên AB//PQ và AB=PQ
Xét tứ giác ABPQ có
AB//PQ(cmt)
AB=PQ(cmt)
Do đó: ABPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)
c) Ta có: MN//BC(cmt)
mà H∈BC(gt)
và P∈BC(P là trung điểm của BC)
nên MN//HP
Xét ΔABC có
M là trung điểm của AB(gt)
P là trung điểm của BC(gt)
Do đó: MP là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒MP//AC và \(MP=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Ta có: ΔAHC vuông tại H(AH⊥BC)
mà HN là đường trung tuyến ứng với cạnh huyền AC(N là trung điểm của AC)
nên \(HN=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Từ (1) và (2) suy ra MP=HN
Xét tứ giác MNPH có MN//HP(cmt)
nên MNPH là hình thang có hai đáy là MN và HP(Định nghĩa hình thang)
Hình thang MNPH(MN//HP) có MP=HN(cmt)
nên MNPH là hình thang cân(Dấu hiệu nhận biết hình thang cân)

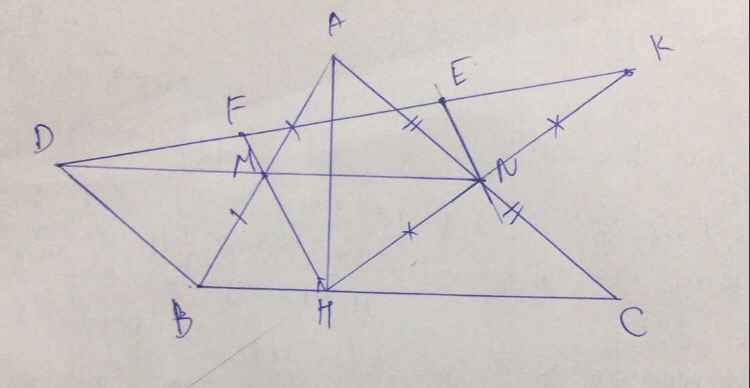
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
Xét tứ giác BDNC có
DN//BC
BD//NC
Do đó: BDNC là hình bình hành
b: Xét tứ giác BDNH có BH//DN
nên BDNH là hình thang
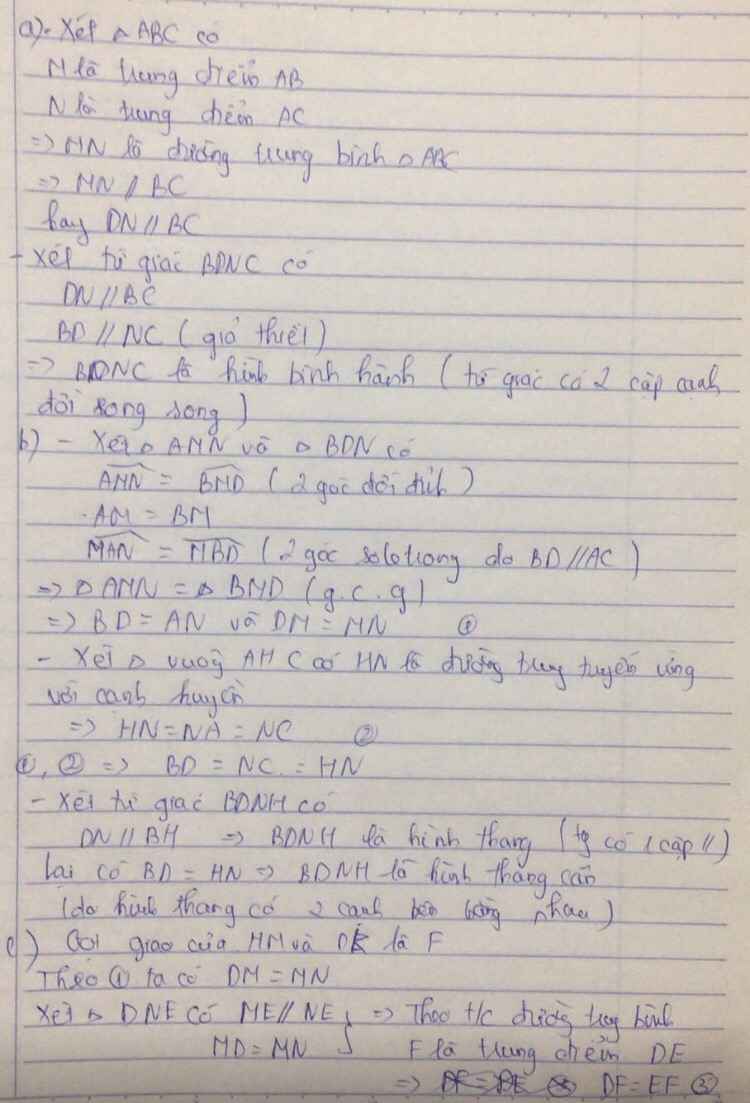
a: Xét tứ giác APCQ có
N là trung điểm chung của AC và PQ
nên APCQ là hình bình hành
=>AQ//CP và AQ=CP
AQ=CP
CP=PB
Do đó: AQ=BP
AQ//CP
mà B thuộc tia đối của tia CP
nên AQ//BP
Xét tứ giác AQPB có
AQ//PB
AQ=PB
Do đó: AQPB là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC
=>MN//HP
Xét ΔABC có
M,P lần lượt là trung điểm của BA,BC
=>MP là đường trung bình
=>MP//AC và MP=AC/2(1)
ΔAHC vuông tại H
mà HN là đường trung tuyến
nên \(HN=\dfrac{AC}{2}\)(2)
Từ (1),(2) suy ra MP=HN
Xét tứ giác MNPH có
MN//PH
MP=HN
Do đó: MNPH là hình thang cân