Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông tại A có
\(cosB=\dfrac{AB}{BC}\)
=>\(\dfrac{4}{BC}=sin60=\dfrac{1}{2}\)
=>BC=8(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+4^2=8^2=64\)
=>\(AC^2=48\)
=>\(AC=4\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot4\cdot4\sqrt{3}=8\sqrt{3}\)
Nửa chu vi tam giác ABC là:
\(4+4\sqrt{3}+8=12+4\sqrt{3}\)
Bán kính đường tròn nội tiếp ΔABC là:
\(\dfrac{8\sqrt{3}}{12+4\sqrt{3}}=\dfrac{2\sqrt{3}}{\sqrt{3}+3}=\sqrt{3}-1\)

a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)

\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)
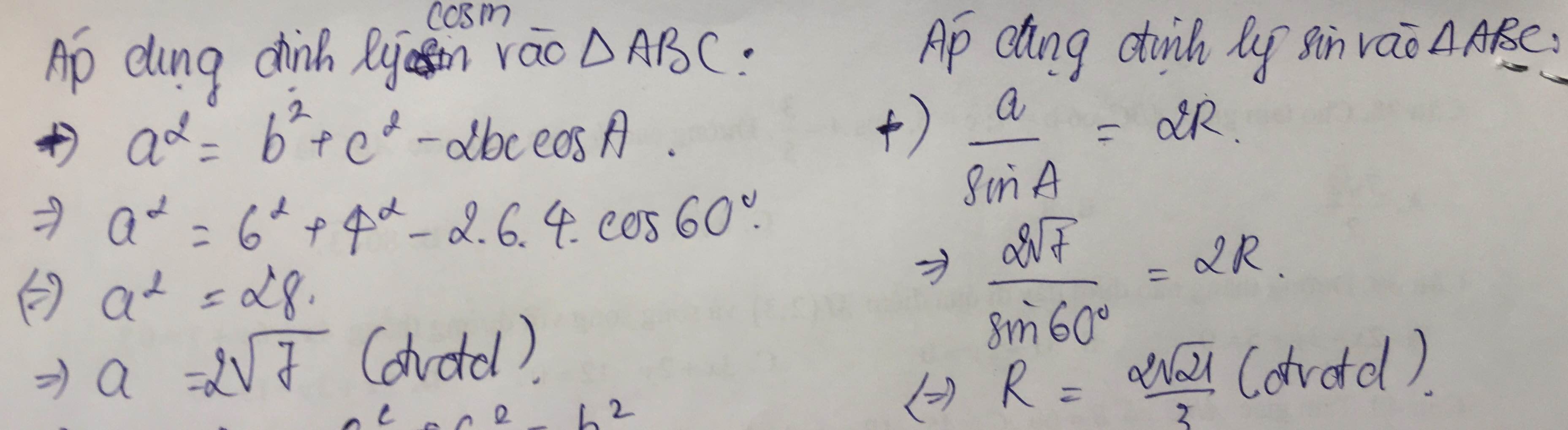
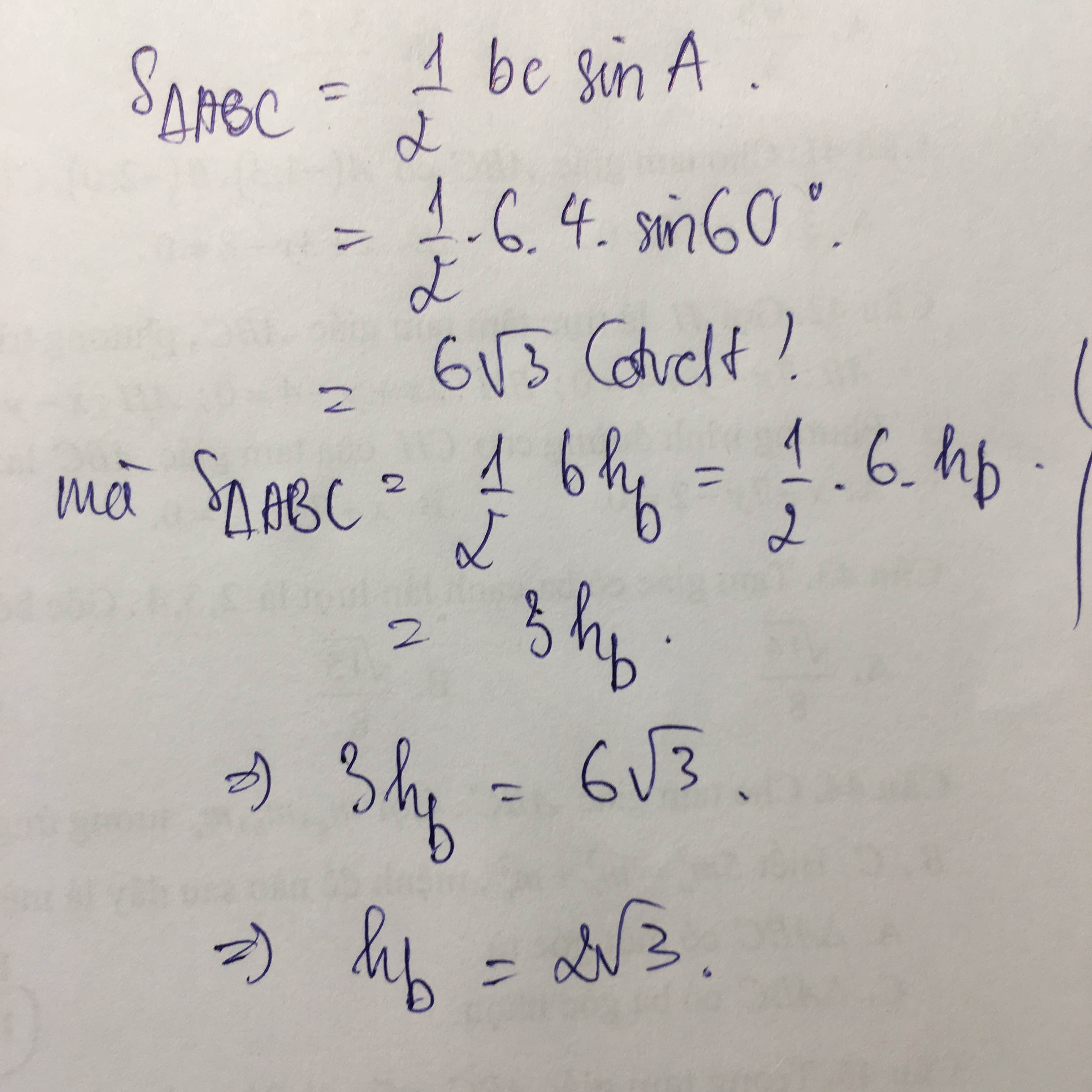
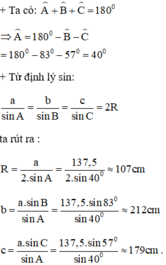
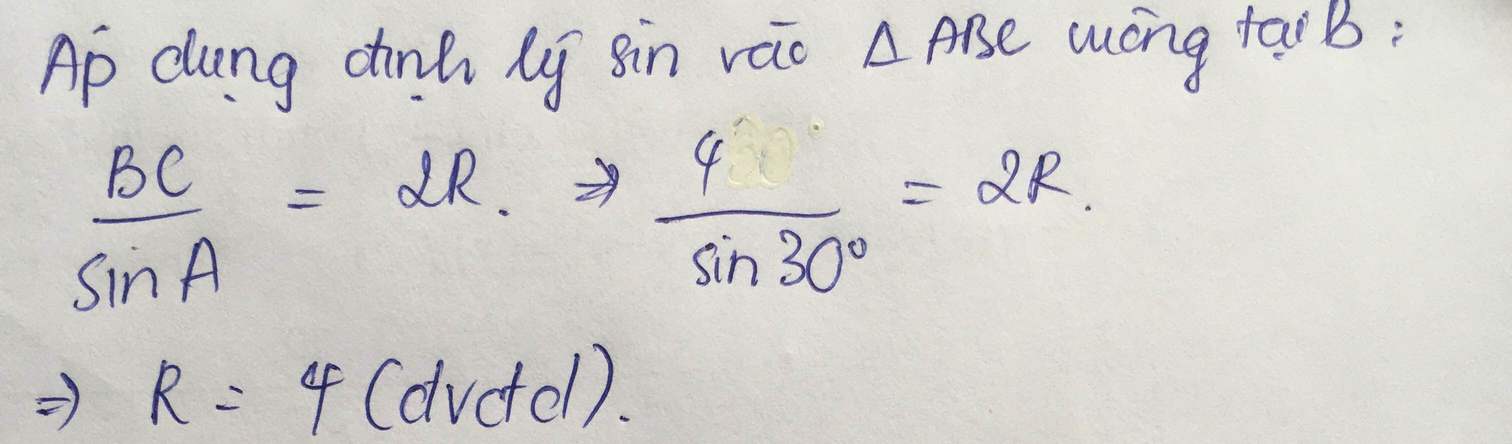
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+45^0+105^0=180^0\)
=>\(\widehat{BAC}=30^0\)
=>\(\widehat{BAD}=\widehat{CAD}=15^0\)
Xét ΔADB có \(\widehat{BAD}+\widehat{ABD}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}=180^0-15^0-45^0=120^0\)
Xét ΔADB có
\(\dfrac{AB}{sinADB}=\dfrac{AD}{sinB}\)
=>\(\dfrac{AB}{sin120}=\dfrac{4}{sin45}=4:\dfrac{\sqrt{2}}{2}=4\sqrt{2}\)
=>\(AB=2\sqrt{6}\)
Xét ΔABC có \(\dfrac{AB}{sinC}=2R\)
=>\(2R=\dfrac{2\sqrt{6}}{sin105}=12-4\sqrt{3}\)
=>\(R=6-2\sqrt{3}\)