Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
=>DB=DE
b: ΔABD=ΔAED
nên góc BDA=góc EDA
=>DA là phân giác của góc BDE
c: Xét ΔDBI và ΔDEC có
BI=EC
góc DBI=góc DEC
DB=DE
Do đó: ΔDBI=DEC
=>góc BDI=góc EDC
=>góc BDI+góc BDE=180 độ
=>I,D,E thẳng hàng

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
=>\(\widehat{ABD}=\widehat{AED}\) và DB=DE
Xét ΔAEF và ΔABC có
\(\widehat{AEF}=\widehat{ABC}\)
AE=AB
\(\widehat{EAF}\) chung
Do đó: ΔAEF=ΔABC
=>AC=AF

\(\text{#TNam}\)
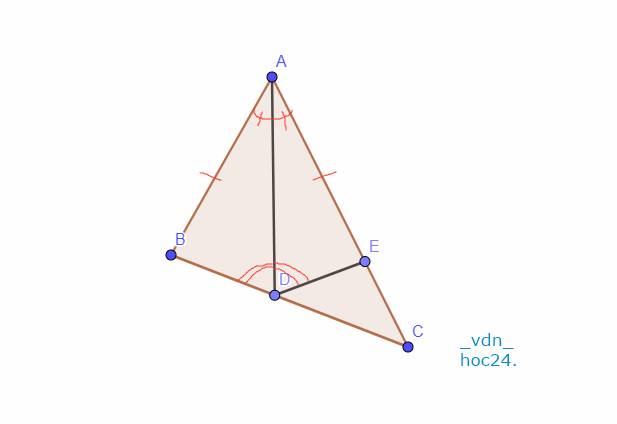
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)

1:
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
b: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC

Xét t/g ABD và t/g AHD có:
AB = AH (gt)
góc BAD = góc DAH (gt)
AD : cạnh chung
Do đó t/g ABD = t/g AHD (c.g.c)
=> góc ABD = góc AHD (2 góc tương ứng)
Mà góc ABD = 90 độ
=> góc AHD = 90 độ
Vậy AC _|_ DH
Chứng minh được ΔAHD=ΔABD(c.g.c)⇒∠AHD = ∠ABD = 900ΔAHD=ΔABD(c.g.c)⇒∠AHD = ∠ABD = 900(hai góc tương ứng).
Vậy DH ⊥⊥AC.