Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình tự vẽ nka :D
xét tam giác ABD và tam giác AMD có
AD chung
A1=A2
AB = AM
=> tam giác ABD = tam giác AMD ( c.g.c)
=> DM = BD

a) Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)(BM là tia phân giác của \(\widehat{ABD}\))
Do đó: ΔBAM=ΔBDM(cạnh huyền-góc nhọn)
Suy ra: BA=BD(hai cạnh tương ứng)
Xét ΔABD có BA=BD(cmt)
nên ΔABD cân tại B(Định nghĩa tam giác cân)
b) Ta có: ΔBAM=ΔBDM(cmt)
nên MA=MD(hai cạnh tương ứng)
Ta có: BA=BD(cmt)
nên B nằm trên đường trung trực của AD(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MA=MD(cmt)
nên M nằm trên đường trung trực của AD(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BM là đường trung trực của AD(Đpcm)
c) Xét ΔAME vuông tại A và ΔDMC vuông tại D có
MA=MD(cmt)
\(\widehat{AME}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔAME=ΔDMC(cạnh góc vuông-góc nhọn kề)
Suy ra: ME=MC(hai cạnh tương ứng)
Xét ΔMEC có ME=MC(cmt)
nên ΔMEC cân tại M(Định nghĩa tam giác cân)
d) Ta có: ΔAME=ΔDMC(cmt)
nên AE=DC(hai cạnh tương ứng)
Ta có: BA+AE=BE(A nằm giữa B và E)
BD+DC=BC(D nằm giữa B và C)
mà BA=BD(cmt)
và AE=DC(cmt)
nên BE=BC
Xét ΔBEC có BE=BC(cmt)
nên ΔBEC cân tại B(Định nghĩa tam giác cân)
hay \(\widehat{BEC}=\dfrac{180^0-\widehat{EBC}}{2}\)(Số đo của một góc ở đáy trong ΔBEC cân tại B)(3)
Ta có: ΔBAD cân tại B(cmt)
\(\Leftrightarrow\widehat{BAD}=\dfrac{180^0-\widehat{ABD}}{2}\)(Số đo của một góc ở đáy trong ΔBDA cân tại B)
hay \(\widehat{BAD}=\dfrac{180^0-\widehat{EBC}}{2}\)(4)
Từ (3) và (4) suy ra \(\widehat{BAD}=\widehat{BEC}\)
mà \(\widehat{BAD}\) và \(\widehat{BEC}\) là hai góc ở vị trí đồng vị
nên AD//EC(Dấu hiệu nhận biết hai đường thẳng song song)

a: Xét ΔADB và ΔADM có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔADB=ΔADM
b: Ta có: ΔADB=ΔADM
nên DB=DM
mà AB=AM
nên AD là đường trung trực của BM
c: Xét ΔBDN và ΔMDC có
\(\widehat{BDN}=\widehat{MDC}\)
DB=DM
\(\widehat{DBN}=\widehat{DMC}\)
Do đó: ΔBDN=ΔMDC
Suy ra: BN=MC
Ta có: AB+BN=AN
AM+MC=AC
mà AB=AM
và BN=MC
nên AN=AC
hay ΔANC cân tại A

b) Vì AC=2AB
AB=BD
=>AC=AD
Xét tam giác ACE và tam giác ADE có:
AC=AD ( chứng minh trên )
^CAE=^EAD ( tính chất phân giác )
AE chung
=> tam giác ACE = tam giác ADE ( c.g.c )
=> ^CEA=^AED ( 2 góc tương ứng )
Mà ^CEA kề bù ^AED
=> ^CEA=^AED=90°
=> AE vuông góc CD
AI và AE là 2 tia trùng nhau
=> AI vuông góc CD
Vì AI vuông góc BM
Mà AI vuông góc CD
<=> BM // CD
Chúc bạn học tốt!
Vì mình không tìm được cách gõ góc nên kí hiệu ^ là góc nhé! Mong bạn thông cảm

a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC

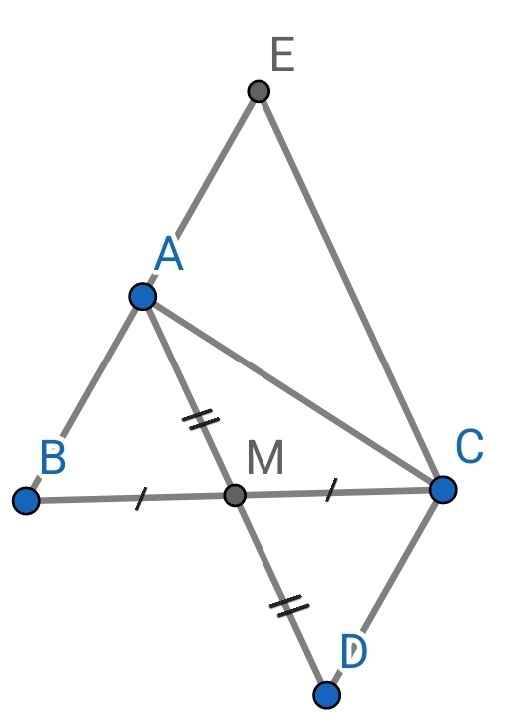 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE

a: Xét ΔABD và ΔAMD có
AB=AM
góc BAD=góc MAD
AD chung
Do đó; ΔABD=ΔAMD
b: Xét ΔDBN và ΔDMC có
góc DBN=góc DMC
DB=DM
góc BDN=góc MDC
Do đó; ΔDBN=ΔDMC
=>BN=MC
c: Xét ΔANC có AB/BN=AM/MC
nên BM//CN