Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC có AB = AC => Tam giác ABC cân tại A
=> AH vừa là đường trung tuyến vừa là tia phân giác góc BAC
b) Vì tam giác ABC cân tại A (cmt)
=> AH cũng là đường cao
=> AH vuông góc BC
c) Xét tứ giác ABCK có
H là trung điểm BC (gt)
H là trung điểm AK (gt)
=> Tứ giác ABCK là hình bình hành
=> CK // AB

a, Xét tam gác ABH và tam giác ACH có:
AB=AC (gt)
BH=CH
AH là cạnh chung
=> tam giác ABH=ACH ( c.c.c)
=> góc BAH = CAH ( hai góc tương ứng )
Vì tam giác ABC là tam giác cân mà AH vừa là trung điểm vừa là tia phân giác thì AH cũng là đường cao của ta giác ABC => AH vuông góc vs BC
b, Xét tam giác vuông ABH và tam giác vuông KCH có :
BH=CH (gt)
HK=HA (gt)
=> tam giác vuông ABH = tam giác vuông KCH ( hai cạnh góc vuông )
=> góc HAB = góc HKC ( hai góc tương ứng )
Vì góc HAB = góc HKC nên CK//AB ( cặp góc sole trong )

dũng có 1 túi bi . dũng lấy ra 1/5 số bi và thêm 2 viên nữa thì được 10 viên .tính số bi trong túi của Dũng ?

\(a,\left\{{}\begin{matrix}AB=AC\\BH=HC\\AH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\\ \Rightarrow\widehat{BAH}=\widehat{CAH}\\ \Rightarrow AH\text{ là p/g }\widehat{BAC}\\ \Delta AHB=\Delta AHC\Rightarrow\widehat{AHB}=\widehat{AHC}\\ \text{Mà }\widehat{AHC}+\widehat{AHB}=180^0\\ \Rightarrow\widehat{AHC}=\widehat{AHB}=90^0\\ \Rightarrow AH\bot BC\)
\(b,\left\{{}\begin{matrix}HK=HA\\BH=HC\\\widehat{AHB}=\widehat{KHC}\left(\text{đối đỉnh}\right)\end{matrix}\right.\Rightarrow\Delta AHB=\Delta KHC\left(c.g.c\right)\\ \Rightarrow\widehat{ABH}=\widehat{HCK}\\ \text{Mà 2 góc này ở vị trí so le trong nên }CK\text{//}AB\\ c,\text{Đề lỗi}\)

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của \(\widehat{BAC}\)
b: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AH là đường trung trực của BC
hay AH\(\perp\)BC
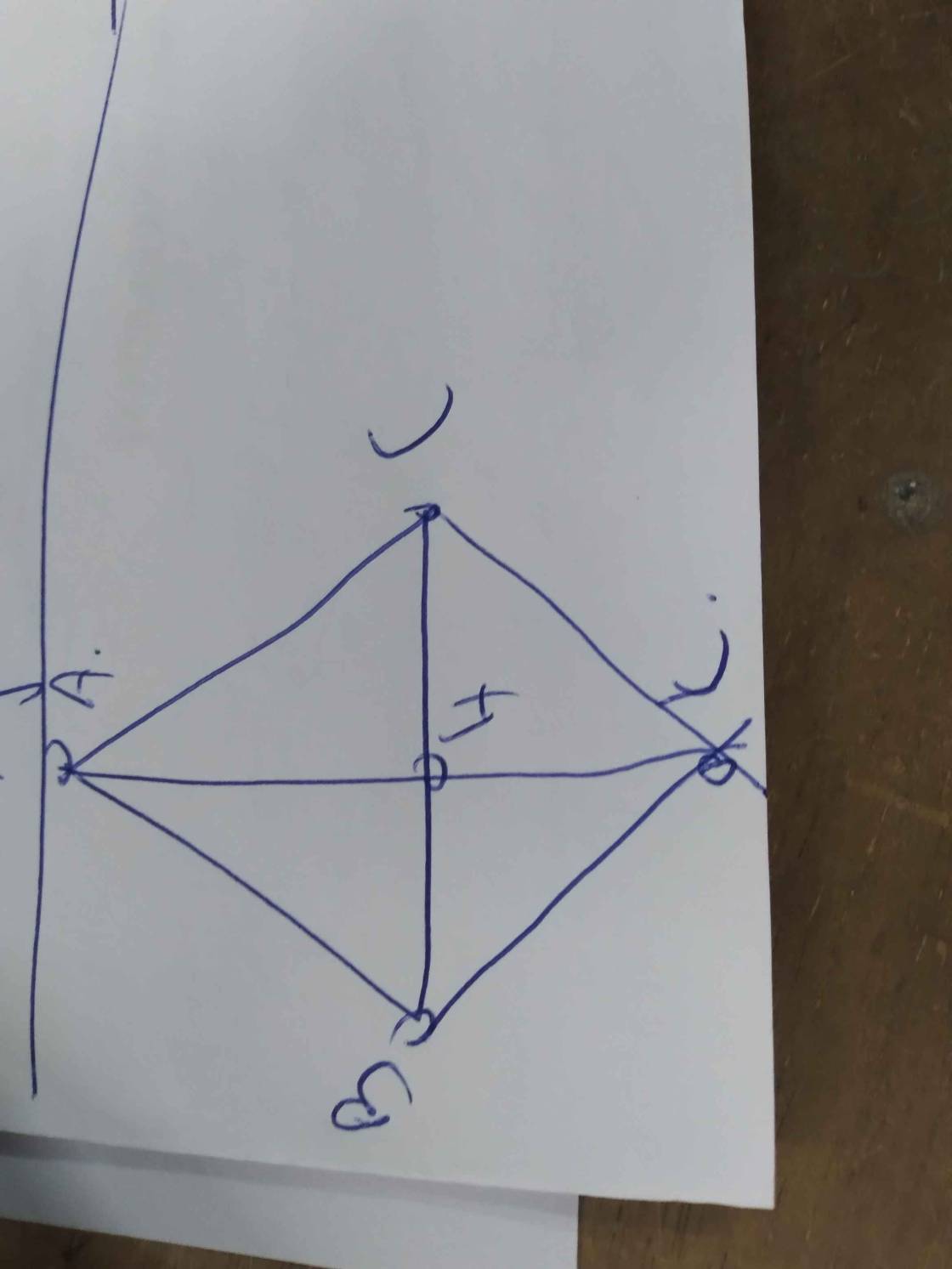


a) Xét tam giác AHB và tam giác AHC có :
AB=AC ( gt )
BH = HC ( vì H là trung điểm của cạnh BC )
AH : cạnh chung
do đó tam giác AHB = tam giác AHC ( c.c.c )
suy ra góc BAH = HAC ( 2 góc t/ứ )
nên AH là tia phân giác của góc BAC
b) Có tam giác AHB = tam giác AHC ( c/m trên )
suy ra góc BHA = góc CHA ( 2 góc t/ứ )
mà B , H , C thẳng hàng
suy ra góc BHC là góc bẹt
suy ra góc BHA = góc CHA = 90 độ
nên AH vuông góc với BC