Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABC có AB = AC nên tam giác ABC cân tại A
\(\Delta ABE\)= \(\Delta ACD\) ( cgc ) ( AB = AC (gt) ; \(\widehat{B}\) =\(\widehat{C}\) ( tam giác ABC cân tại A) ; BE = CD = \(\frac{2}{3}\) BC )
Do đó \(\widehat{BAE}\) = \(\widehat{DAC}\) => tam giác DAE cân tại A
b) tam giác ABC cân tại A có AM là đường trung tuyến => AM là đường cao của tam giác ABC .
Tam giác DAE cân tại A có AM là đường cao ứng với cạnh DE => AM là đường phân giác của tam giác DAE => AM là tia phân giác của \(\widehat{DAE}\)
c) Tam giác DAE cân tại A có \(\widehat{DAE}\) = 600 => Tam giác DAE là tam giác đều => mỗi góc trong tam giác DAE đều là 600

a, Ta có : BD=DE=EC(gt)
=>BD+DE=DE+EC
hay BE=DC
Xét Tam giác EAB Và DAC có:
BE=DC(đã cm)
AB=AC(gt)
Góc ABE=góc ACD( tg ABC cân vì AB=AC)
=>tg EAB=TgDAC(cgc)
=>EA^B=DA^C=>đpcm
có tg ABC cân tại A
AM là đường trung tuyến( m là trung điểm BC)
=> AM đồng thời là đường cao của tg ABC=> ^M1( góc AMB)= ^M2( góc AMC)=90*
Xét tg ADM và tg AEM có:
AD=AE(gt)
M1=M2=90*(đã cm)
cạnh AM chung
=> tg ADM=Tg AEM(cạnh huyền-cạnh góc vuông)
=>^DAM=^EAM
=> AM là tia pg góc......=>đpcm

a, Xét tam giác EAB và tam giác DAC có:
AB = AC (gt)
AD = AE (gt)
BE = CD (BE = BD + DE = DE + EC = CD)
=> Tam giác EAB = Tam giác DAC (c.c.c)
b,M là trung điểm của BC
=> AM là đường trung tuyến của tam giác ABC cân tại A (AB = AC)
=> AM là đường cao của tam giác ABC
hay AM _I_ BC
mà D, E thuộc BC
=> AM _I_ DE
hay AM là đường cao của tam giác ADE cân tại A (AD = AE)
=> AM là tia phân giác của DAE
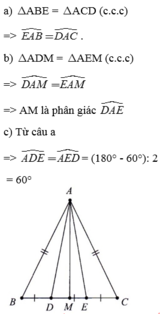
a: Xét ΔEAB và ΔDAC có
AE=AD
AB=AC
EB=DC
Do đó: ΔEAB=ΔDAC
Suy ra: \(\widehat{EAB}=\widehat{DAC}\)
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là đường phân giác