TC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
11 tháng 3 2023
Ta có AB/AE = AC/AF
<=> 6/4=9/6=3/2
AEF và ABC chung góc A
=> AEF và ABC đồng dạng "cạnh góc cạnh "
b) BC =3x3/2=4,5cm
BF
11 tháng 3 2023
`a)` Ta có: `(AE)/(AB) = 4/6 = 2/3`
`(AF)/(AC) = 6/9 = 2/3`
`=> (AE)/(AB) = (AF)/(AC)`
Xét `ΔAEF` và `ΔABC` có:
`hat{A}` chung
`(AE)/(AB) = (AF)/(AC)`
`=> ΔAEF ∼ ΔABC (c - g - c) ` (đpcm)
`b) ` Theo `a) ΔAEF ∼ ΔABC `
`=> (EF)/(BC) = (AF)/(AC)`
`=> 3/(BC) = 2/3`
`=> BC = 3 : 2/3 = 9/2`
Vậy `BC = 9/2cm`
24 tháng 3 2023
Xét \(\Delta ABC\&\Delta ABH\) ta có:
\(\widehat{A}=\widehat{B}=90^o\left(gt\right)\\ \widehat{B}=\widehat{B}\\\Rightarrow \Delta ABC\&\sim ABH\)
KV
24 tháng 3 2023
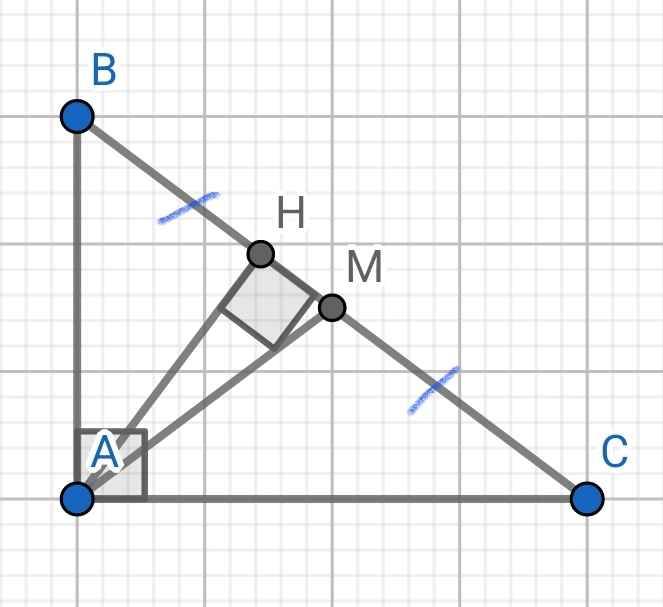
Xét ∆AHB và ∆CBA có:
∠AHB = ∠CAB = 90⁰
∠B chung
⇒ ∆AHB ∽ ∆CBA (g-g)
1 tháng 3 2022
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔACB có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó:BD=30/7cm; CD=40/7cm
21 tháng 3 2021
a) Ta có: \(BC^2=5^2=25\)
\(AB^2+AC^2=3^2+4^2=25\)
Do đó: \(BC^2=AB^2+AC^2\)(=25)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
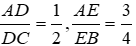
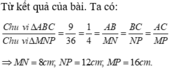
chu vi tam giác ABC là
( 3 x 4 ) : 2 = 6 cm2
AC k phải BC