K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

22 tháng 2 2022
Bài 1:
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
Ta có: AE+EB=AB
AD+DC=AC
mà AB=AC
và AD=AE
nên EB=DC
Xét ΔEBO vuông tại E và ΔDCO vuông tại D có
EB=DC
\(\widehat{EBO}=\widehat{DCO}\)
Do đó: ΔEBO=ΔDCO
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
DO đó:ΔABO=ΔACO
Suy ra: \(\widehat{BAO}=\widehat{CAO}\)
hay AO là tia phân giác của góc BAC
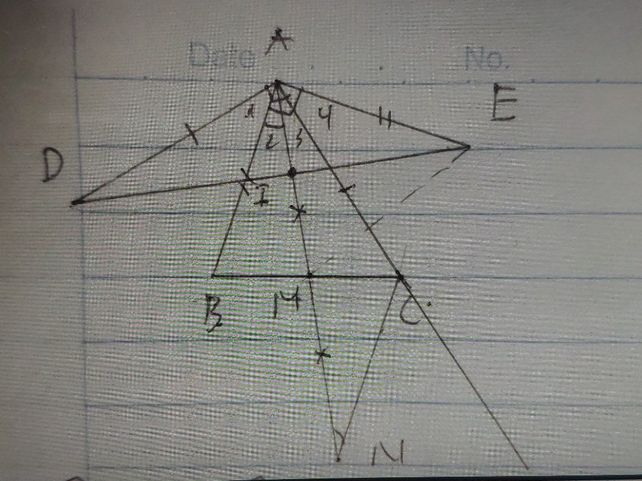

a) Xét \(\bigtriangleup BCE \) và \(\bigtriangleup CBD\) có:
\(EC=BD\left(gt\right)\)
\(\widehat{ECB}=\widehat{CBD}\)(2 góc sole trong do BD//CE)
\(BC-chung\)
\(\implies \bigtriangleup BCE=\bigtriangleup CBD(c.g.c)\)
b) Có: \(\bigtriangleup BCE=\bigtriangleup CBD(cmt)\)
\(\implies EB=CD\)(1)
Có: AB=CD(gt)
\(\Rightarrow\frac{1}{2}AB=\frac{1}{2}CD\Rightarrow EB=CF\)(2)
Từ (1) và (2) \(\implies CD=CF\)
Có: AB=CD(gt)
\(\implies \bigtriangleup ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(2 góc ở đáy)
Xét \(\bigtriangleup ECB\) và \(\bigtriangleup FBC\) có:
\(EB=FC(cmt)\)
\(\widehat{EBC}=\widehat{FCB}\left(cmt\right)\)
\(BC-chung\)
\(\implies \bigtriangleup ECB=\bigtriangleup FBC(c.g.c)\)
\(\implies BF=CE\)(2 cạnh tương ứng)
c) Có: \(\bigtriangleup BCE= \bigtriangleup CBD\)
\(\Rightarrow\widehat{EBC}=\widehat{DCB}\)
Gọi FD giao BC tại N
Xét \(\Delta FCN\) và \(\Delta DCN\) có;
\(CF=CD\)(câu b)
\(\widehat{FCN}=\widehat{DCN}\left(cmt\right)\)
\(CN-chung\)
\(\Rightarrow\Delta FCN=\Delta DCN\left(c.g.c\right)\)
\(\Rightarrow\widehat{CNF}=\widehat{CND}\)(2 góc tương ứng)
Mà \(\widehat{CNF}+\widehat{CND}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{CNF}=\widehat{CND}=90^o\Rightarrow FD\perp BC\)
d) Xét \(\Delta EMC\) và \(\Delta DMB\) có:
\(EC=BD\left(gt\right)\)
\(\widehat{ECM}=\widehat{MBD}\)
\(MB=MC\)(vì M-trung điểm BC)
\(\Rightarrow\Delta EMC=\Delta DMB\left(c.g.c\right)\)
\(\Rightarrow\widehat{EMC}=\widehat{DMB}\)(2 góc tương ứng)
Mà \(\widehat{BME}+\widehat{EMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{BME}+\widehat{DMB}=180^o\)
\(\Rightarrow EM\equiv MD\)
\(\implies E;M;D\) thẳng hàng
_Học tốt_
d) Ta có EC // BD và EC = BD ( tam giác BCE = tam giác CBD )
=> tứ giác BECD là hình bình hành
=> ED giao BC tại trung điểm mỗi đường
Mà M là trung điểm của BC nên M là trung điểm của ED
=> M, E, D thẳng hàng ( đpcm )