Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.

\(a,BC^2=AB^2+AC^2\Rightarrow\Delta ABC\) vuông tại A
\(b,\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\\ AH=\dfrac{AB\cdot AC}{BC}=3,6\left(cm\right)\\ c,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot6\cdot4,5=13,5\)

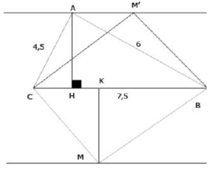
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
![]()
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
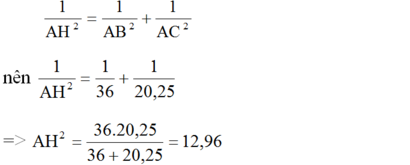
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
![]()
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

a) Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A ( đpcm )
Ta có : \(tgB=\frac{AC}{AB}=\frac{4,5}{6}=0,75\)
\(\Rightarrow\widehat{B}=37^o\)
\(\Rightarrow\widehat{C}=90^o-\widehat{B}=90^o-37^o=53^o\)
Mặt khác trong tam giác ABC vuông tại A, ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
nên \(\frac{1}{AH^2}=\frac{1}{36}+\frac{1}{20,25}\)
\(\Rightarrow AH^2=\frac{36.20,25}{36+20,25}=12,96\)
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có :
\(S_{ABC}=\frac{1}{2}AH.BC\)và \(S_{MBC}=\frac{1}{2}MK.BC\)
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình ).

a)ta thấy AB^2+AC^2=56.25 và BC^2=56.25
=>AB^2+BC^2=BC^2<=>tam jác ABC vuông tại A
Sin B=AC/BC=4.5/7.5<=>B=36độ 52 phút 11.63 giây (bấm shift sin 4.5/7.5 =)
sin c=AB/BC =>C=53đô 7 phút 48.37 giây
Sin C=AH/Ac =>AH=sin C*AC=3.6
b)qua A kẻ đường thẳng d song song BC.diện tích tam jác ABC luôn bằng diện tích tam jác BMC khi M thuộc d.(vì MH sẽ luôn = AH

a, Áp dụng hệ thức giữa cạnh và đường cao trong các tam giác vuông

∆AHC và ∆AHB ta có:
AE.AC = A H 2 = AD.AB => ∆AHC ~ ∆AHB(c.g.c)
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ∆ABC tính được AH = 3cm => DE = 3cm
Trong ∆AHB vuông ta có:
tan A B C ^ = A H H B => A B C ^ ≈ 56 0 , S A D E = 27 13 c m 2
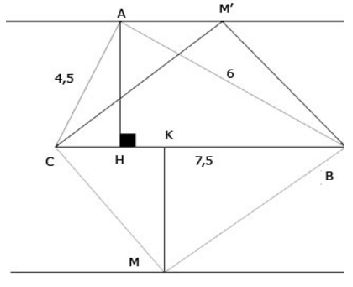
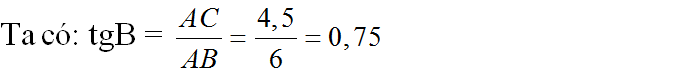
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)