Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

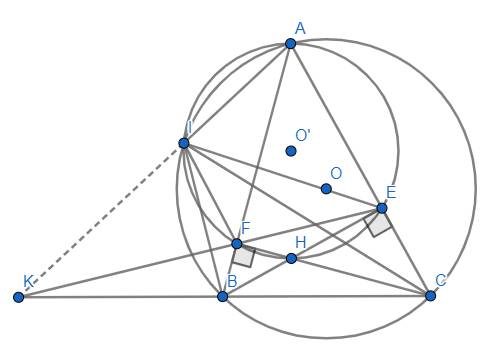
(a) Gọi \(O'\) là tâm đường tròn ngoại tiếp tứ giác \(AIFE.\)
Ta có : \(\hat{IEF}=\hat{IAF}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{IEF}=\hat{IAB}.\)
Mà : \(\hat{IAB}=\hat{ICB}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(IB\)).
Do đó, \(\hat{IEF}=\hat{ICB}.\)
Ta cũng có : \(\hat{FIE}=\hat{FAE}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{FIE}=\hat{BAC}.\)
Mà : \(\hat{BAC}=\hat{BIC}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(BC\)).
Do đó, \(\hat{FIE}=\hat{BIC}.\)
Xét \(\Delta IBC,\Delta IFE:\left\{{}\begin{matrix}\hat{ICB}=\hat{IEF}\left(cmt\right)\\\hat{BIC}=\hat{FIE}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta IBE\sim\Delta IFE\left(g.g\right)\) (đpcm).
(b) Mình tạm thời chưa nghĩ ra nhé:)

Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5