Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.

Gọi \(H\left(x;y\right)\) là trực tâm tam giác
\(\Rightarrow\overrightarrow{AH}=\left(x+3;y\right)\) ; \(\overrightarrow{BH}=\left(x-3;y\right)\); \(\overrightarrow{BC}=\left(-1;6\right)\) ; \(\overrightarrow{AC}=\left(5;6\right)\)
Do H là trực tâm tam giác \(\Rightarrow\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-\left(x+3\right)+6y=0\\5\left(x-3\right)+6y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x+6y=3\\5x+6y=15\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{5}{6}\\\end{matrix}\right.\) \(\Rightarrow H\left(2;\dfrac{5}{6}\right)\)

a: \(\overrightarrow{AB}=\left(-3;4\right)\)
\(\overrightarrow{AC}=\left(8;6\right)\)
Vì \(\overrightarrow{AB}\cdot\overrightarrow{AC}=0\) nên ΔABC vuông tại A
c: Tọa độ trọng tâm G là:
\(\left\{{}\begin{matrix}x_G=\dfrac{1-2+9}{3}=\dfrac{8}{3}\\y_G=\dfrac{2+6+8}{3}=\dfrac{16}{3}\end{matrix}\right.\)

Ta có:
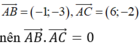
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.

Gọi trực tâm là H
\(\overrightarrow{BC}=\left(1;1\right)\)
\(\overrightarrow{AH}=\left(x-2;y-1\right)\)
Theo đề, ta có: (x-2)*1+1(y-1)=0
=>x+y-3=0
\(\overrightarrow{AC}=\left(-2;3\right)\)
\(\overrightarrow{BH}=\left(x+1;y-3\right)\)
Theo đề, ta có; -2(x+1)+3(y-3)=0
=>-2x-2+3y-9=0
=>-2x+3y=11
mà x+y=3
nên x=-2/5; y=17/5
Gọi (C): \(x^2+y^2-2ax-2by+c=0\) là phương trình đường tròn ngoại tiếp ΔABC
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}2^2+1^2-4a-2b+c=0\\1+9+2a-6b+c=0\\0^2+4^2+0a-8b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4a-2b+c=-5\\2a-6b+c=-10\\-8b+c=-16\end{matrix}\right.\)
=>a=7/10; b=23/10; c=12/5
=>x^2+y^2-7/5x-23/5x+12/5=0
=>x^2-2*x*7/10+49/100+y^2-2*x*23/10+529/100=169/50
=>(x-7/10)^2+(y-23/10)^2=169/50
=>R=13/5căn 2

\(\overrightarrow{AB}=\left(4;0\right)\)
\(\overrightarrow{AC}=\left(3;3\right)\)
\(\cos\widehat{A}=\dfrac{4\cdot3+3\cdot0}{\sqrt{4^2}+\sqrt{3^2+3^2}}=\dfrac{12}{4+3\sqrt{2}}=-24+18\sqrt{2}\)
=>Đề sai rồi bạn
a: A(3;1); B(2;6); C(4;-1)
\(AB=\sqrt{\left(2-3\right)^2+\left(6-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)
\(AC=\sqrt{\left(4-3\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
\(BC=\sqrt{\left(4-2\right)^2+\left(-1-6\right)^2}=\sqrt{2^2+7^2}=\sqrt{53}\)
Chu vi tam giác ABC là:
\(C_{ABC}=\sqrt{26}+\sqrt{5}+\sqrt{53}\left(đvđd\right)\)
b: Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+5-53}{2\cdot\sqrt{26\cdot5}}\simeq-0,96\)
=>\(\widehat{A}\simeq165^0\)
c: Gọi H(x,y) là trực tâm của ΔABC
\(\overrightarrow{AH}=\left(x-3;y-1\right)\)
\(\overrightarrow{BH}=\left(x-2;y-6\right)\)
\(\overrightarrow{BC}=\left(2;-7\right);\overrightarrow{AC}=\left(1;-2\right)\)
H là trực tâm nên ta có: AH\(\perp\)BC và BH\(\perp\)AC
=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x-3\right)+\left(-7\right)\left(y-1\right)=0\\1\left(x-2\right)+\left(-2\right)\left(y-6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-6-7y+7=0\\x-2-2y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-7y=-1\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-7y=-1\\2x-4y=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-1+20=19\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{19}{3}\\x=-10+2y=-10-\dfrac{38}{3}=-\dfrac{68}{3}\end{matrix}\right.\)