Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có:
\(\left\{\begin{matrix}
\frac{x_A+x_B+x_C}{3}=x_G\\
\frac{y_A+y_B+y_C}{3}=y_G\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x_C=3x_G-x_A-x_B\\
y_C=3y_G-y_A-y_B\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x_C=3.2-(-2)-0=8\\ y_C=3.3-0-4=5\end{matrix}\right.\)
Vậy tọa độ điểm $C$ là $(8,5)$

Từ giả thiết suy ra \(\overrightarrow{AB}=\left(-2;2\right);\overrightarrow{BC}=\left(4;-3\right)\)
Gọi H(x;y) là trực tâm của tam giác ABC thế thì \(\overrightarrow{CH}=\left(x-2;y\right),\overrightarrow{AH}=\left(x;y-1\right)\)
Ta có H là trực tâm của tam giac ABC khi và chỉ khi
\(\begin{cases}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{CH}.\overrightarrow{AB}=0\end{cases}\)\(\Leftrightarrow\) \(\begin{cases}4x-3\left(y-1\right)=0\\-2\left(x-2\right)+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=-9\\y=-11\end{cases}\)
Vậy trực tâm của tam giác ABC là H(-9;-11)
Để tìm tọa độ của tâm I đường tròn ngoại tiếp tam giác ABC ta có thể sử dụng công thức khoảng cách IA=IB=IC hoặc sử dụng đẳng thức Vecto \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{IH}\)
Hoặc cũng có thể làm như sau :
Gọi M và N theo thứ tự là trung điểm của AB và BC. Khi đó M(-1;2) và \(N\left(0;\frac{3}{2}\right)\)
Gọi I(x;y) là tâm đường tròn ngoại tiếp của tam giác. Khi đó :
\(\begin{cases}\overrightarrow{IM}.\overrightarrow{AB}=0\\\overrightarrow{IN}.\overrightarrow{BC}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-2\left(-1-x\right)+2\left(2-y\right)=0\\4\left(-x\right)-3\left(\frac{3}{2}-y\right)=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{9}{2}\\y=\frac{15}{2}\end{cases}\)
Vậy tâm đường tròn ngoại tiếp của tam giác ABC là \(I\left(\frac{9}{2};\frac{15}{2}\right)\)

a.
\(\overrightarrow{BC}=\left(2;-3\right)\Rightarrow\) đường thẳng BC nhận (3;2) là 1 vtpt
Phương trình BC:
\(3\left(x-2\right)+2\left(y-3\right)=0\Leftrightarrow3x+2y-12=0\)
b.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(\dfrac{7}{3};\dfrac{4}{3}\right)\)
(C) tiếp xúc BC \(\Leftrightarrow d\left(G;BC\right)=R\)
\(\Rightarrow R=\dfrac{\left|3.\dfrac{7}{3}+2.\dfrac{4}{3}-12\right|}{\sqrt{3^2+2^2}}=\dfrac{7\sqrt{13}}{39}\)
Phương trình: \(\left(x-\dfrac{7}{3}\right)^2+\left(y-\dfrac{4}{3}\right)^2=\dfrac{49}{117}\)

a)
– Tọa độ trọng tâm G của tam giác ABC là:
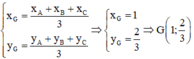
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 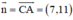 là một vtpt
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 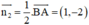 là một vtpt
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
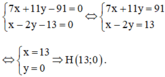
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
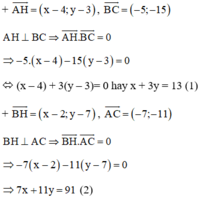
Từ (1) và (2) ta có hệ phương trình
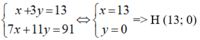
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
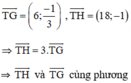
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
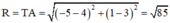
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85

Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=-3\\y_C=3y_G-y_A-y_B=-4\end{matrix}\right.\) \(\Rightarrow C\left(-3;-4\right)\)
\(\Rightarrow\overrightarrow{CA}=\left(4;5\right)\) ; \(\overrightarrow{AB}=\left(1;2\right)\)
Đường cao d đi qua B vuông góc AC nên nhận \(\overrightarrow{CA}=\left(4;5\right)\) là 1 vtpt
Phương trình d:
\(4\left(x-2\right)+5\left(y-3\right)=0\Leftrightarrow4x+5y-23=0\)
Đường cao d1 đi qua C vuông góc AB nên nhận (1;2) là 1 vtpt
Phương trình d1:
\(1\left(x+3\right)+2\left(y+4\right)=0\Leftrightarrow x+2y+11=0\)
H là giao điểm d và d1 nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}4x+5y-23=0\\x+2y+11=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{101}{3}\\y=-\dfrac{67}{3}\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{101}{3};-\dfrac{67}{3}\right)\)

a) Từ giả thiết suy ra \(\overrightarrow{AB}=\left(2;2\right);\overrightarrow{BC}=\left(-1;-5\right)\)
Do \(2:\left(-1\right)\ne2:\left(-5\right)\) nên A, B, C không thẳng hàng hay A, B, C là ba đỉnh của một tam giác
b)
- Gọi \(G\left(x_1;y_1\right)\) là trọng tâm của tam giác ABC.
Khi đó \(x_1=\frac{1+3+3}{3}=2\) và \(y_1=\frac{2+4+\left(-1\right)}{3}=\frac{5}{3}\)
Suy ra \(G\left(2;\frac{5}{3}\right)\)
- Gọi \(H\left(x_2,y_2\right)\) là trực tâm của tam giác ABC. Khi đó H thỏa mãn :
\(\begin{cases}AH\perp BC\\CH\perp AB\end{cases}\) \(\Rightarrow\begin{cases}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{CH}.\overrightarrow{AB}=0\end{cases}\)
Từ đó, ta có hệ
\(\begin{cases}x_2+5y_2-6=0\\x_2+y_2-1=0\end{cases}\)
Giải hệ thu được ( \(x_2;y_2\)) \(=\left(-\frac{3}{4};\frac{7}{4}\right)\) do đó \(H\left(-\frac{3}{4};\frac{7}{4}\right)\)
- Gọi \(I\left(x_3,y_3\right)\) là tâm đường tròn ngoại tiếp tam giác ABC,
do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{IH}\) nên ta có hệ :
\(\begin{cases}1-x_3+3-x_3+2-x_3=-\frac{3}{4}-x_3\\2-y_4+4-y_3-1-y_3=\frac{7}{4}-y_3\end{cases}\)
Giải hệ ta thu được \(\left(x_3,y_3\right)=\left(\frac{27}{8};\frac{13}{8}\right)\)
Do đó \(I\left(\frac{27}{8};\frac{13}{8}\right)\)


Gọi M là trung điểm của BC, vì G là trọng tâm của tam giác ABC nên \(\overrightarrow{AM}=\dfrac{3}{2}\overrightarrow{AG}\)
Có \(\overrightarrow{AG}=\left(0;-3\right);\overrightarrow{AM}=\left(x_M-2;y_M-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_M-2=0\\y_M-3=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=2\\y_M=0\end{matrix}\right.\Rightarrow M\left(2;0\right)\)
\(\overrightarrow{AH}=\left(-1;-2\right)\Rightarrow u_{BC}=\left(1;2\right)\\ BC:1.\left(x-2\right)+2.\left(y-0\right)\\ BC:x+2y-2=0\)
Gọi điểm B có tọa độ theo tham số t, tìm điểm C theo tham số t thông qua điểm M.
Có: \(\overrightarrow{AB}.\overrightarrow{CH}=0\)
Giải phương trình tìm ra t.
Từ đó suy ra tọa độ điểm B và C