Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM(cmt)
CH=CM(cmt)
BC chung
Do đó: ΔBHC=ΔBMC(c-c-c)

a) M đối xứng H qua BC
-> BC là đường trung trực MH
-> CH = CM ; BH = BM
Xét tam giác BHC và tam giác BMC:
CH = CM (cmt)
BC : chung
BH = BM (cmt)
-> Tam giác BHC = tam giác BMC (c-c-c)
b) Xét tứ giác ADHG:
\(\widehat{A}+\widehat{AGH}+\widehat{ADH}+\widehat{GHD}=360^o\)
\(\rightarrow\widehat{GHD}=360^o-\widehat{A}-\widehat{AGH}-\widehat{ADH}\)
\(\rightarrow\widehat{GHD}=360^o-60^o-90^o-90^o=120^o\)
\(\rightarrow\widehat{GHD}=\widehat{BHC}=120^o\)( đối đỉnh )
Mà \(\widehat{BHC}=\widehat{BMC}\)( tam giác BHC = tam giác BMC )
\(\rightarrow\widehat{BMC}=120^o\)

a: Ta có: M và H đối xứng nhau qua BC
nên BC là đường trung trực của MH
Suy ra: BM=BH; CM=CH
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC

a: Ta có: M và H đối xứng nhau qua BC
nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC

a) Chứng minh được DBHC = DBMC (c.c.c).
b) Gọi {C'} = CH Ç AB. Sử dụng định lý tổng 4 góc trong tứ giác AB'HC' ta tính được B ' H C ' ^ = 120 0
Ta có B ' H C ' ^ = B H C ^ (đối đỉnh) và B C H ^ = B M C ^ ( d o △ B H C = △ B M C ) ⇒ B M C ^ = 120 0
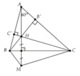

a,ta có :M đối xứng vs H qua BC
suy ra BC là đường trung trực của đoạn thẳng BC
mà B thuộc đường trung trực của đoạn thẳng BC =>BM=BH
và C thuộc đường trung trực của đoạn thẳng BC =>CM=CH
xét tam giác BMC và tam giác BHC có:BM=BH (chứng minh trên),MC=MH chứng minh trên BC chung
=> tam giác BMC=BHC
b,trọng tâm gica ABC có AM là đường trung trực đồng thời là đường cao của cạnh BC => tam giác ABC cân
=>góc ABC =góc BCA =(180 độ -60 độ ):2=60 độ
mà BM và CM là đường phân giác (tam giác ABC cân)suy ra góc MBC =góc MBC =60 độ :2=30 độ
=>góc BMC=180 độ -30 độ+30 độ=120độ
mà góc BCM=góc BCH =>góc BHC=120độ

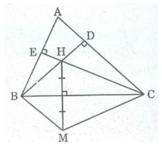
Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM (t/chất đường trung trực)
CH = CM (t/chất đường trung trực)
Xét tam giác BHC và tam giác BMC có:
BC chung
BH= BM ( chứng minh trên)
CH = CM (chứng minh trên)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)
