Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GT ∆ABC cân tại A, AH BC
KL AHB = AHC
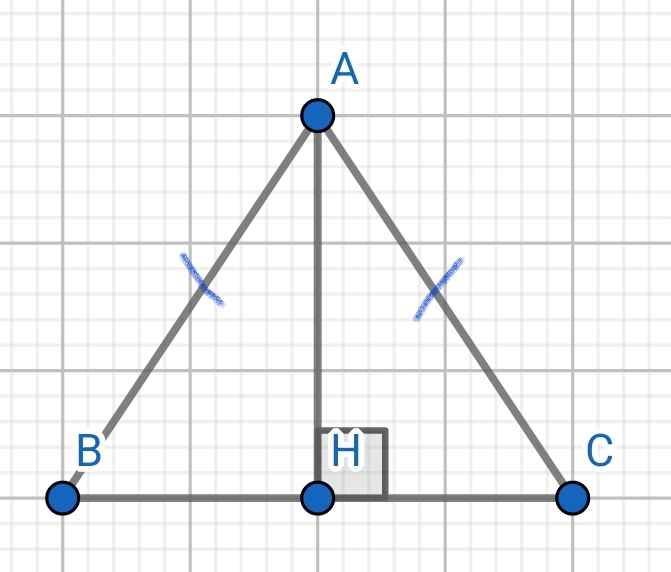
Xét hai tam giác vuông: ∆AHB và ∆AHC có:
AH chung
AB = AC (∆ABC cân tại A)
⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)

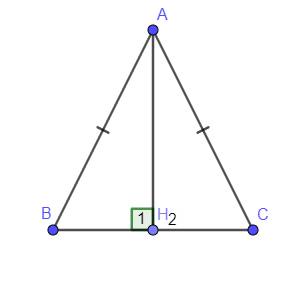
Có `AH⊥BC(GT)=>hat(H_1)=hat(H_2)(=90^0`
`Delta ABC` cân tại `A=>AB=AC`
Xét `Delta AHB` và `Delta AHC` có :
`{:(hat(H_1)=hat(H_2)(=90^0)),(AB=AC(cmt)),(AH-chung):}}`
`=>Delta AHB=Delta AHC(ch-cgv)(đpcm)`

1)A) vì \(\Delta ABC\)CÓ \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\Delta ABC\)CÂN TẠI A
\(\Rightarrow AB=AC\)
XÉT \(\Delta ADB\)VÀ\(\Delta ADC\)CÓ
\(AB=AC\left(CMT\right)\)
\(\widehat{ADB}=\widehat{ADC}\left(GT\right)\)
\(AD\)LÀ CẠNH CHUNG
\(\Rightarrow\Delta ADB=\Delta ADC\left(C-G-C\right)\)
B)VÌ\(\Delta ABC\)CÓ \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\Delta ABC\)CÂN TẠI A
=> AB=AC

a: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó;ΔABC=ΔADC
Suy ra: CB=CD
hay ΔCBD cân tại C
c: Xét ΔCBD có
CA là đường trung tuyến
CE=2/3CA
Do đó: E là trọng tâm của ΔCBD
=>DE đi qua trung điểm của BC

c: Xét tứ giác BHDM có
A là trung điểm chung của BD và HM
=>BHDM là hình bình hành
=>BH//DM
ta có:BH//DM
H\(\in\)BC
Do đó: DM//BC
d: Ta có: ΔCBD cân tại C
mà CA là đường cao
nên CA là phân giác của góc BCD
Xét ΔCNA vuông tại N và ΔCHA vuông tại H có
CA chung
\(\widehat{NCA}=\widehat{HCA}\)
Do đó: ΔCNA=ΔCHA
=>NA=AH
mà AH=1/2HM
nên NA=1/2HM
Xét ΔNHM có
NA là đường trung tuyến
\(NA=\dfrac{1}{2}HM\)
Do đó: ΔNHM vuông tại N

b: Ta có: ΔAIE cân tại A
mà AK là đường phân giác
nên K là trung điểm của EI
hay KE=KI
c: Xét ΔAID và ΔAED có
AI=AE
\(\widehat{IAD}=\widehat{EAD}\)
AD chung
Do đó: ΔAID=ΔAED
Suy ra: \(\widehat{AID}=\widehat{AED}=90^0\)
=>DE⊥AB
mà AC⊥AB
nên DE//AC

Xét ΔADB vuông tại B và ΔADC vuông tại C có
AD chung
AB=AC
Do đó: ΔADB=ΔADC
Suy ra: DB=DC
mà AB=AC
nên AD là đường trung trực của BC
hay AD\(\perp\)BC

b: Xét ΔEAK và ΔIAK có
AE=AI
\(\widehat{EAK}=\widehat{IAK}\)
AK chung
Do đó: ΔEAK=ΔIAK
Suy ra: KE=KI
Cảm ơn nhá :}