Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

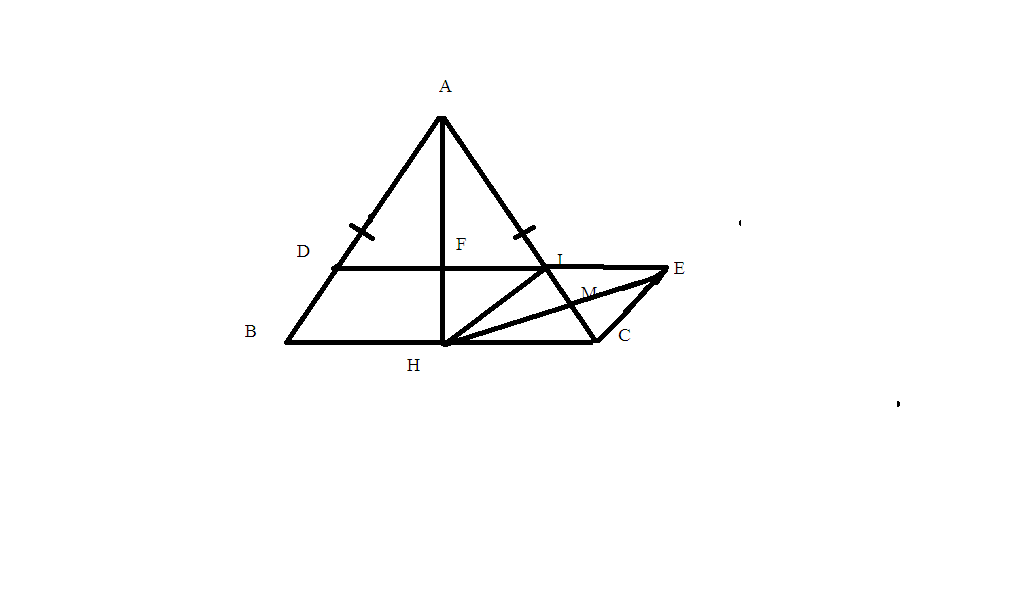
a) Xét ΔABH và ΔACH có:
AB=AC (ΔABC cân tại A)
AH là cạnh chung
HB=HC(H là trung điểm của BC)
Nên ΔABH =ΔACH (c.c.c)
=>\(\widehat{AHB}=\widehat{AHC}\)( 2 GÓC TƯƠNG ỨNG)
Ta có: \(\widehat{AHB}+\widehat{AHC}=180^O\)( 2 góc kề bù)
=>\(\widehat{AHB}.2=180^O\Rightarrow\widehat{AHB}=90^O\)
=>AH ⊥ BC
b) Vì ΔABH =ΔACH => \(\widehat{BAH}=\widehat{CAH}\)
Ta có: AD+BD=AB ( D nằm giữa A và B)
AI+IC=AC( I nằm giữa A và C)
Mà AB=AC, BD=IC =>AD=AI
Cho AH và DI cắt nhau tại F
Xét ΔDFA và ΔIFA có:
FA là cạnh chung
\(\widehat{BAH}=\widehat{CAH}\)
AD=AI
Nên ΔDFA=ΔIFA (c.g.c)
=>\(\widehat{DAF}=\widehat{IAF}\)
=>A là tia phân giác của góc DHI

a, sét tam giác ABH và tam giác ACH có: AB=AC(gt); góc ABC= góc ACB(gt); BH=CH(gt)
suy ra 2 tam giác đó bằng nhau
suy ra góc AHB=góc AHC=180 độ chia 2=90 độ
hay AH vuông góc vs BC
b, xét tam giác ADH và tam giác AIH có: góc DAH = góc IAH(do tam giác ABH= tam giác ACH); AD=AI (do AB=AC;BD=CI); AH chung
suy ra 2 tam giác đó bằng nhau
suy ra góc DHA= góc IHA
suy ra đpcm


ghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
mấy bạn bớt nhắn linh tinh lên đây đi, olm là nơi học bài và hỏi bài chứ không phải nhắn lung tung

hình bạn tự vẽ nha
a) trong △ABC có :
AH⊥BC=> AH là đường cao của △ABC
mà △ABC cân tại A
=>AH vừa là đường cao , vừa là đường trung tuyến của △ABC
b)có △ABC cân tại A=> góc ABC=góc ACB
hay góc DBH=góc ACB
mà: HD//AC
=>góc BHD=góc ACB(ĐV)
=> góc DBH=gócBHD
=>△BHD cân tại D
=> BD=DH(1)
có AH⊥BC => △ABH vuông tại H
=> góc BAH+góc ABH=900
mà góc BHD+ góc HAD =900; góc ABH= góc DHB
=>góc DAH= góc DHA
=>△AHD cân tại D
=> DA=DH(2)
từ (1),(2)=> AD=DB(=DH)
=> D là trung điểm của AB
c)trong △ABC có:
AH là đường trung tuyến thứ nhất của △ABC
D là trung điểm của AB=> CD là đường trung tuyến thứ hai của △ABC
E là trung điểm của AC=>BE là đường trung tuyến thứ ba của △ABC
lại có AH và CD cắt nhau tại G
=> G là trọng tâm của △ABC
=> BE đi qua G
=> 3 điểm B,G,E thẳng hàng




