Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.

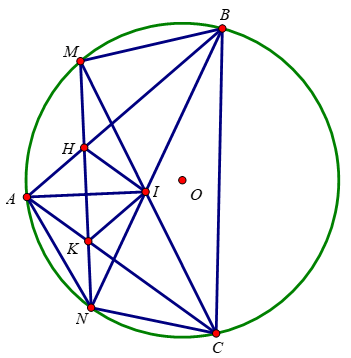
a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA

a/
BC=√(AB^2+AC^2)=√9^2+12^2)=3√9+16)=3.5=15
b
AG=2/3AM=2/3.1/2.BC=5

Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).

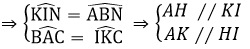
a: AM=AB/2
AN=AC/2
mà AB=AC
nên AM=AN
b: Xét tứ giác AGCK có
N là trung điểm của AC
N là trung điểm của GK
Do đó: AGCK là hình bình hành
Suy ra: AG//CK
c: Xét ΔABC có
BN là đường trung tuyến
CM là đường trung tuyến
BN cắt CM tại G
Do đó: G là trọng tâm của ΔABC
Suy ra: BG=2GN
mà GK=2GN
nên BG=GK