Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

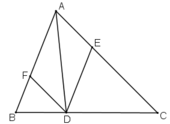
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a: Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Do đó: DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BDEC là hình thang cân

Bạn tự vẽ hình nha ==''
AD = AE
=> Tam giác ADE cân tại A
=> ADE = 900 - DAE/2
mà ABC = 900 - BAC/2 (tam giác ABC cân tại A)
=> ADE = ABC
mà 2 góc này ở vị trí so le trong
=> DE // BC
=> BDEC là hình thang
mà ABC = ACB (tam giác ABC cân tại A)
=> BDEC là hình thang cân
BD = DE
=> Tam giác DBE cân tại D
=> DBE = DEB
mà DEB = EBC (DE // BC, 2 góc so le trong)
=> DBE = EBC
=> BE là tia phân giác của DBC
DE = EC
=> Tam giác ECD cân tại E
=> ECD = EDC
mà EDC = DCB (DE // BC, 2 góc so le trong)
=> ECD = DCB
=> CD là tia phân giác của ECB
Vậy BD = DE = EC <=> D và E lần lượt thuộc tia phân giác của DBC và ECB

làm câu A trước : ( hình tự vẽ )
a) Vì AD = AE ( gt )
\(\Rightarrow\)t/g ADE cân tại A
\(\Rightarrow\)\(\widehat{D1}=\frac{180-\widehat{A}}{2}\)( t/g ABC cân tại A )
\(\widehat{B}=\frac{180-\widehat{A}}{2}\) ( t/g ABC cân tại A )
\(\Rightarrow\widehat{D1}=\widehat{B}\)vài 2 góc này ở vị trí đồng vị
\(\Rightarrow\)DE // BC
\(\Rightarrow\)BDEC - httg
Ta có : \(\widehat{B}=\widehat{C}\) ( t/g ABC cân tại A )
\(\Rightarrow\)BDEC - httg cân
a: Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
s
7