Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AK=AH
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
e: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AH=AK
Do đó: ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
Suy ra: BH=CK

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC
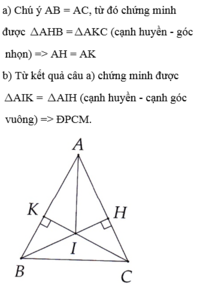
Bạn tự vẽ hình nhé
Ta có : \(\widehat{BHC}=\widehat{CKB}=90^o\)
mà \(\widehat{HCB}=\widehat{KBC}\)
=> \(\widehat{BHC}-\widehat{HCB}=\widehat{CKB}-\widehat{KBC}\)
<=> \(\widehat{KCB}=\widehat{HBC}\)
Xét tam giác vuông HCB và tam giác vuông KCB
BC là cạnh huyền chung
\(\widehat{KCB}=\widehat{HBC}\)(cmt)
=> tam giác HCB bằng với tam giác KCB ( cạnh huyền góc nhọn)
=> KB =HC
mà AB =AC ( tam giác ABC cân tại A)
=> AB-KB=AC-HC = AK=AH => Tam giác AKH cân tại A => \(\widehat{AHK}=\frac{180^o-\widehat{KAH}}{2}\)
Tam giác ABC cân tại A => \(\widehat{ACB}=\frac{180^o-\widehat{BAC}}{2}\)
mà \(\frac{180^o-\widehat{KAH}}{2}=\frac{180^o-\widehat{BAC}}{2}\)
=> \(\widehat{AHK}=\widehat{ACB}\)
mà 2 góc trên ở vị trí so le trong => KH song song với BC