Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình bạn tự vẽ nhé
dựng tam giác AMN đều , nối M với C , N với C
Xét tam giác ABC và tam giác CAN có
AM=AN=BC
AC chung
góc CAN=góc ACB=40 độ
\(\Rightarrow\)tam giác ABC=tam giác CAN ( c.g.c)
\(\Rightarrow\)CN=AB=AC
Xét tam giác CMN và tam giác CMA có
AM=MN
AC=NC
CM chung
\(\Rightarrow\)tam giác CMN = tam giác CMA ( c.c.c)
\(\Rightarrow\)góc AMC=góc NMC=\(\frac{1}{2}\)góc AMN=30 độ

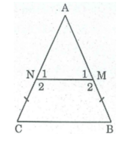
∠ B = ∠ C = ( 180 0 – 40 0 ) / 2 = 70 0
Mà ∠ M 2 + ∠ B = 180 0 (hai góc trong cùng phía nên bù nhau)
Suy ra: ∠ M 2 = 180 0 - ∠ B = 180 0 – 70 0 = 110 0
∠ N 2 = ∠ M 2 = 110 0 (tính chất hình thang cân)

Phần a thì mình có thể làm được nhưng phần b thì hơi sai sai á bạn.
Bạn xem lại đề nha.

1) a) vì tam giác ABC cân tại a --> góc B = Góc C = (180 - 50 ) :2 = 65 độ b) vì AD=AE --> tam giác ADE cân tại A. mà gốc A= 50 độ --> góc D = góc E= 65 độ . --> góc D= Góc B ( vì cùng bằng 65 độ ) mà 2 góc này là 2 góc đồng vị của 2 đường thẳng DE và BC nên DE // BC 2) a ) vì tam giác ABC cân --> AB=AC (1 mà AD=AE ( gt) (2) và BD = AB - AD (3) , EC= AC - AE (4) Từ (1) (2) (3) (4) --> BD= EC b) ta có góc ABC = AC (vì tam giác ABC cân tại A ) hay góc DBC = góc ECB xét tam giác DBC và tan giác ECB có : +) DBC=ECB ( cmt) +) DB=EC ( CM phần a ) + ) cạnh BC chung nên tam giác DBC = tam giac ECB ( cgc)--> EBC= DCB ( 2 góc tương ứng ) hay OBC = OCB --> tam giác OBC cân tại O chứng minh DE// BC như bài 1 --> ODE = OED --> tam giác ODE cân tại O ( Bài 2 này em cứ làm phần c trước nhé em để nó ngắn em à ) 3)a) Ta có tam giác ABC vuông tại A --> góc ABC+ góc ACB = 90 độ mà ABC = 60 đôh ( gt) --> ACB = 30 độ ta lại có Cx vuông góc với BC tại c --> BCx = ACB + ACx = 90 độ makf ACB = 30 độ --> ACx = 60 độ (1) và AC = AE (gt) (2) từ (1) và (2) --> tam giavc ACE là tam giác đều b) ta có ABF = 120 độ ( Vì là góc kề bù của góc ABC =60 độ ) tam giác ABF có AB=BF (gt) --> tam giác ABF cân tại B --> BÀ =BFA= 9 180 - 120 ) : 2 = 30 độ vì tam giác ACE là tam giác đều -- EAC = 60 độ ta có EAF = EAC + CAF + BAF = 60 + 90 + 30 = 180 độ --> 3 điểm E , A F thẳng hàng

a)
Xét tam giác BAC vuông tại A và tam giác BMN vuông tại M có:
\(\widehat{BAC}\)=\(\widehat{BMN}\)
=> Tam giác BAC ᔕ Tam giác BMN (g-g)
=> BA/BM=BC/BN
=> BN=BM.\(\dfrac{BC}{BA}\)=18.\(\dfrac{20}{12}\)=30cm
b)
Xét tam giác PAN vuông tại A và tam giác PMC vuông tại M có
\(\widehat{APN}\)=\(\widehat{MPC}\) (đối đỉnh)
=> Tam giác PAN ᔕ Tam giác PMC (g-g)
=> \(\dfrac{PA}{PM}\)=\(\dfrac{PN}{PC}\)
=> PA.PC=PM.PN (đpcm)
Theo bài ra, ta có \(\widehat{B}=\widehat{C}=40^o\)
\(\Rightarrow\widehat{A}=100^o\)
\(\Rightarrow\widehat{CBM}=100+40=180^o\)(TC góc ngoài tam giác)
Lại có \(BC=BM\Rightarrow\)Tam giác BMC cân tại B
\(\Rightarrow\widehat{BMC}=\widehat{BCM}=\left(180-140\right):2=20^o\)
Vậy AMC = 20 độ
À, nhầm chỗ góc CBM là 140 độ bạn nhé, không phải 180 độ đâu, mình đánh nhầm, còn lại phía dưới vẫn đúng bạn nhé