Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

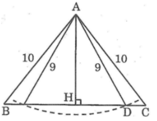
Kẻ AH ⊥ AB.
Xét hai tam giác vuông AHB và AHC, ta có:
∠AHB = ∠AHC = 90o
AB = AC (gt)
AH cạnh chung
Suy ra: ΔAHB = ΔAHC
(cạnh huyền - cạnh góc vuông)
Suy ra: HB = HC (hai cạnh tương ứng)
Ta có: HB = HC = BC/2 = 6 (cm)
Trong tam giác vuông AHB có ∠AHB = 90o
Áp dụng định lí Pi-ta-go, ta có:
AB2 = AH2 + HB2 ⇒ AH2 = AB2 – HB2 = 102 – 62 = 64
⇒ AH = 8 (cm)
Do bán kính cung tròn 9(cm) > 8(cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC.
Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm với BC.
Vì đường xiên AD < AC nên hình chiếu HD < HC.
Do đó D nằm giữa H và C.
Vậy cung tròn tâm A bán kính 9 cm cắt cạnh BC.

Kẻ AH vuông góc với BC
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó; ΔAHB=ΔAHC
Suy ra: HB=HC=BC/2=6(cm)
=>AH=8(cm)
Vì R=9cm nên cung tròn này cắt đường thẳng CB
Gọi D là giao điểm của (A;9cm) với BC
Vì AD<AC nên HD<HC
=>D nằm giữa H và C
hay cung tròn này cắt cạnh BC

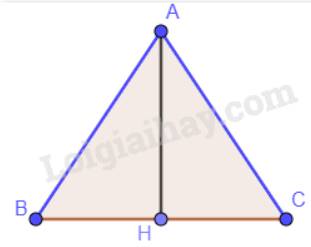
a) Tam giác ABC cân tại A nên AB = AC. Vậy điểm A có thuộc đường trung trực của đoạn thẳng BC.
b) Ta có tam giác ABC cân mà đường thẳng qua A vuông góc với BC cắt BC tại H nên H là trung điểm của BC.
Vậy AH là đường trung trực của đoạn thẳng BC. (AH đi qua trung điểm H của đoạn thẳng BC và vuông góc với đoạn thẳng BC).

Tham khảo
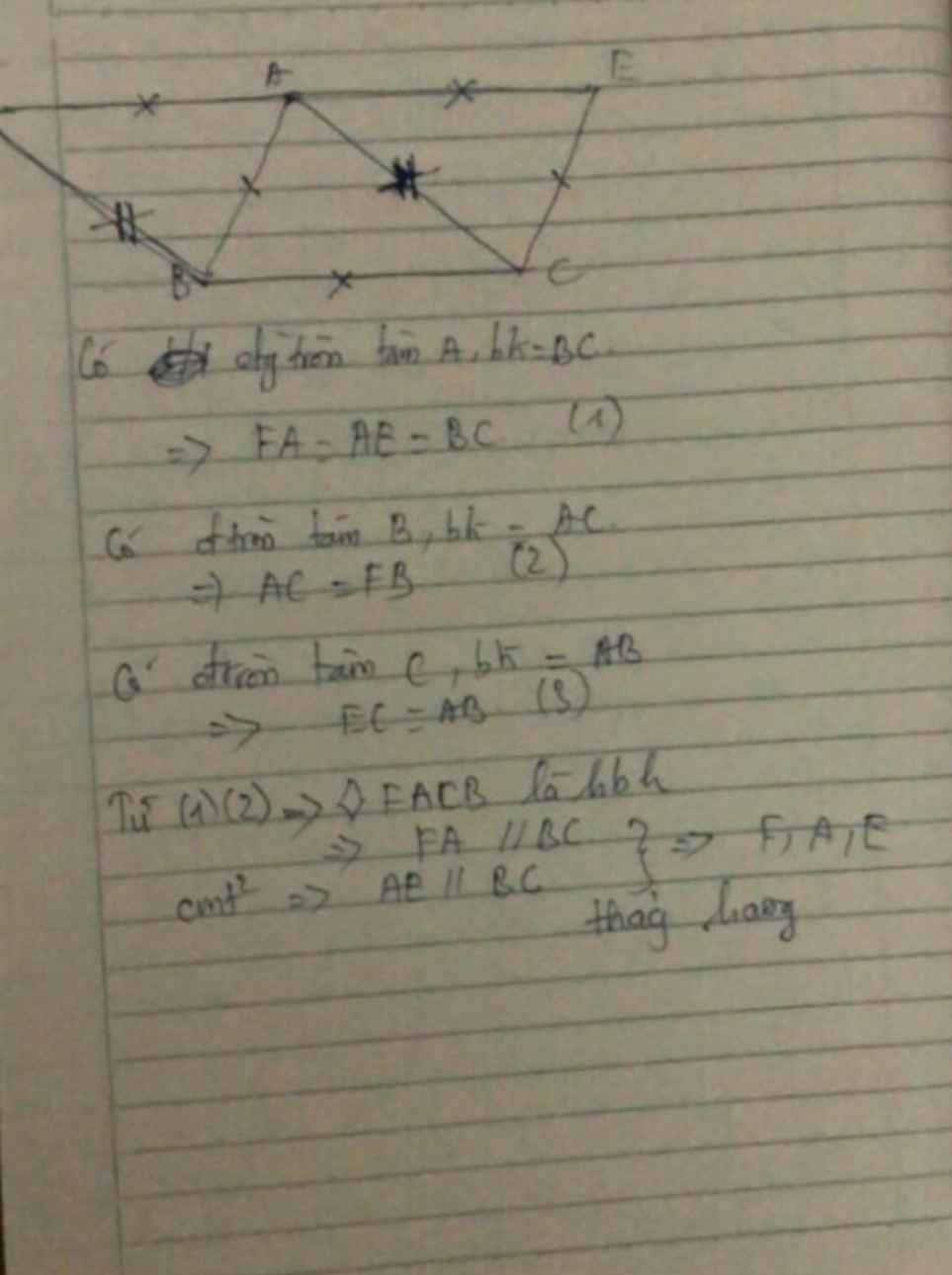
ΔΔABC và ΔΔDCB có AB=CD (gt)
BC chung AC=DB (gt)
Vậy ΔΔABC = ΔΔDCB (c.c.c)
Suy ra ˆBDC=ˆA=800BDC^=A^=800 (hai góc tương ứng)
b) Do ΔΔABC = ΔΔDCB (câu a) do đó ˆABC=ˆBCDABC^=BCD^ (hai góc tương ứng của hai tam giác bằng nhau)
Hai góc này ở vị trí so le trong của hai đường thẳng AB và CD cắt đường thẳng BC do đó CD // AB.
Hoàng Thị Ngọc Anh giúp mình với
Hoàng Thị Ngọc Anh ( tag hộ )