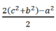Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vẽ chỉ mang tính chất minh họa:
Gọi G là trọng tâm tam giác, P là trung điểm AB
Áp dụng công thức trung tuyến:
\(CP^2=\dfrac{2\left(a^2+b^2\right)-c^2}{4}=\dfrac{10c^2-c^2}{4}=\dfrac{9c^2}{4}\)
\(\Rightarrow CP=\dfrac{3c}{2}\Rightarrow GP=\dfrac{1}{3}CP=\dfrac{c}{2}=\dfrac{AB}{2}=AP=BP\)
\(\Rightarrow\widehat{AGB}\) là góc nội tiếp chắn nửa đường tròn đường kính AB
\(\Rightarrow AM\perp BN\)
Xin phép được chia sẻ 1 cách giải để bạn tham khảo, em cám ơn thầy Nguyễn Việt Lâm luôn nhiệt tình giúp đỡ chúng em ạ

Gọi G là giao điểm của AM và BN.
Theo công thức tính độ dài đường trung tuyến: \(AM^2=\dfrac{2b^2+2c^2-a^2}{4}\);
\(BN^2=\dfrac{2c^2+2a^2-b^2}{4}\).
Từ đó \(AG^2=\dfrac{4}{9}AM^2=\dfrac{2b^2+2c^2-a^2}{9}\); \(BG^2=\dfrac{4}{9}BN^2=\dfrac{2c^2+2a^2-b^2}{9}\).
Do đó \(AG^2+BG^2=\dfrac{a^2+b^2+4c^2}{9}=\dfrac{9c^2}{9}=c^2=AB^2\).
Theo định lý Pythagoras đảo thì tam giác AGB vuông tại G.
Vậy góc giữa 2 trung tuyến AM và BN là 90o.

Chọn A.
+ Vì M là trung điểm của BC nên ![]()
Suy ra ![]()
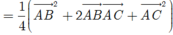
Theo câu trên ta có ![]() nên
nên
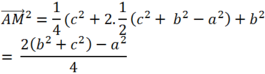

\(BM=\dfrac{1}{2}BC=3\)
\(AM=\sqrt{AB^2+BM^2-2AB.BM.cos60^0}=\sqrt{19}\)
\(BN=\dfrac{\sqrt{2\left(AB^2+BM^2\right)-AM^2}}{2}=\dfrac{7}{2}\)

Lời giải:
$\overrightarrow{CM}.\overrightarrow{BN}=(\overrightarrow{CA}+\overrightarrow{AM})(\overrightarrow{BA}+\overrightarrow{AN})$
$=\overrightarrow{CA}.\overrightarrow{BA}+\overrightarrow{CA}.\overrightarrow{AN}+\overrightarrow{AM}.\overrightarrow{BA}+\overrightarrow{AM}.\overrightarrow{AN}$
$=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{CA}.\frac{1}{4}\overrightarrow{AC}+\frac{1}{5}\overrightarrow{AB}.\overrightarrow{BA}+\frac{1}{5}\overrightarrow{AB}.\frac{1}{4}\overrightarrow{AC}$
$=\frac{21}{20}\overrightarrow{AB}.\overrightarrow{AC}-\frac{1}{4}AC^2-\frac{1}{5}AB^2$
$=\frac{21}{20}\cos A.|\overrightarrow{AB}|.|\overrightarrow{AC}|-\frac{1}{4}AC^2-\frac{1}{5}AB^2$
$=\frac{21}{20}.\frac{1}{2}.5.8-\frac{1}{4}.8^2-\frac{1}{5}.5^2=0$
$\Rightarrow CM\perp BN$

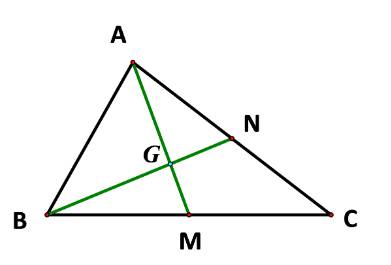
Ta có: \(\overrightarrow {AG} ,\overrightarrow {AM} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right|\)
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} .\) Vậy \(a = \frac{2}{3}.\)
Ta có: \(\overrightarrow {GN} ,\overrightarrow {GB} \)là hai vecto ngược hướng và \[\left| {\overrightarrow {GN} } \right| = \frac{1}{3}BN = \frac{1}{2}.\left( {\frac{2}{3}BN} \right) = \frac{1}{2}\left| {\overrightarrow {GB} } \right|\]
Suy ra \(\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} .\) Vậy \(b = - \frac{1}{2}.\)

\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)\)
=0