Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

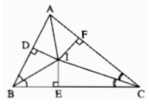
Kẻ: ID⊥AB, IE⊥BC, IF⊥AC
Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:
∠(DBI) =∠(EBI) (gt)
∠(IDB) =∠(IEB) =90o
BI cạnh chung
Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)
Suy ra: ID = IE ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:
∠(ECI) =∠(FCI)
∠(IEC) =∠(IFC) =90o
CI cạnh huyền chung
Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:
ID=IF
∠(IDA) =∠(IFA) =90o
AI cạnh huyền chung
Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)
Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)
Vậy AI là tia phân giác góc A

1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)

Vẽ IH vuông góc AB, IK vuông góc AC, IE vuông góc BC (bạn đặt tên khác cũng được nhưng kẻo nhầm lẫn)
Xét 2 tam giác vuông BIH và BIE có:
BI chung
Góc HBI = góc EBI (BI là phân giác góc B)
=> Tam giác BIH = tam giác BIE (cạnh huyền - góc nhọn)
=> IH = IE (2 cạnh tương ứng) (1)
Xét 2 tam giác vuông KCI và ECI có:
IC chung
Góc KCI = góc ECI (IC là phân giác góc C)
=> Tam giác KCI = tam giác ECI (cạnh huyền - góc nhọn)
=>IK = IE (2 cạnh tương ứng) (2)
Từ (1),(2) => IH = IK (= IE)
Xét 2 tam giác vuông AIH và AIK có:
AI chung
IH = IK (cmt)
=> Tam giác AIH = tam giác AIK (cạnh huyền - cạnh góc vuông)
=> Góc HAI = góc KAI (2 góc tương ứng)
=> AI là tia phân giác góc A

Gọi M,N,P lần lượt là hình chiếu của I lên các cạnh BC,BA,CA
Xét \(\Delta\)BIN và \(\Delta\)BIM có
\(\widehat{IBN}=\widehat{IBM}\)(BI là phân giác)
BI chung
=> \(\Delta\)BIN = \(\Delta\)BIM (cạnh huyền-góc nhọn)
=> IM=IN
CM tương tự có: \(\Delta\)CIP=\(\Delta\)CIM => IM=IP
=> IM=IN=IP
Xét \(\Delta\)AIN và \(\Delta\)AIP vuông tại N và P có:
IA chung
IN=IM
=> \(\Delta\)AIN = \(\Delta\)AIP (cạnh huyền -cạnh góc vuông)
=> \(\widehat{IAN}=\widehat{IAP}\)=> IA là phân giác góc A (DPCM)

4578
Mấy đại ca làm ơn tick giúp em 8 cái tick em đang rất cần

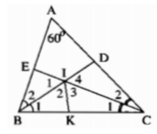
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
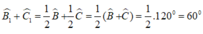
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID
Kẻ ID \(\perp\) AB, IE \(\perp\) BC, IF \(\perp\) AC
Xét hai tam giác vuông IBD và IBE có:
IB: cạnh chung
\(\widehat{DBI}=\widehat{EBI}\) (gt)
Vậy: \(\Delta IBD=\Delta IBE\left(ch-gn\right)\)
\(\Rightarrow\) ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông ICF và ICE có:
IC: cạnh chung
\(\widehat{FCI}=\widehat{ECI}\) (gt)
Vậy: \(\Delta ICF=\Delta ICE\left(ch-gn\right)\)
\(\Rightarrow\) IF = IE (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông AID và AIF có:
AI: cạnh chung
ID = IF (cmt)
Vậy: \(\Delta AID=\Delta AIF\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAD}=\widehat{IAF}\) (hai góc tương ứng)
Do đó: AI là tia phân giác của \(\widehat{A}\).