Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{B}=90^0\)
Xét ΔABC có \(\widehat{C}< \widehat{A}< \widehat{B}\)
nên AB<BC<AC
b: Xét ΔBAC có
BA<BC
mà AH là hình chiếu của BA trên AC
và CH là hình chiếu của BC trên AC
nên AH<CH

a: góc B=góc C=(180-45)/2=67,5 độ
Vì góc A<góc B=góc C
nên BC<AB=AC
b: XetΔAHB vuông tại H và ΔAHC vuông tai H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
c: ΔABC cân tại A
mà AH là đường cao
nên AH là trung trực của BC

a) Xét t/g ABD và t/g HBD có:
AB = BH (gt)
ABD = HBD ( vì BD là phân giác ABC)
BD là cạnh chung
Do đó, t/g ABD = t/g HBD (c.g.c)
=> BAD = BHD = 90o (2 góc tương ứng)
=> DH _|_ BC (đpcm)
b) t/g ABD = t/g HBD (câu a)
=> ADB = HDB (2 góc tương ứng)
Mà ADB + HDB = ADH = 110o
Do đó, ADB = HDB = 110o : 2 = 55o
t/g ABD vuông tại A có: ABD + ADB = 90o
=> ABD + 55o = 90o
=> ABD = 90o - 55o = 35o
k nhé

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Suy ra: DA=DE
a) Vì BD là phân giác của ABC nên ABD = CBD
Xét Δ ABD và Δ EBD có:
BA = BE (gt)
ABD = EBD (cmt)
BD là cạnh chung
Do đó, Δ ABD = Δ EBD (c.g.c)
=> AD = DE (2 cạnh tương ứng) (đpcm)
b) Δ ABD = Δ EBD (câu a) => BAD = BED = 90o (2 góc tương ứng)
=> Δ DEC vuông tại E
Δ ABC vuông tại A có: ABC + C = 90o (1)
Δ CED vuông tại E có: EDC + C = 90o (2)
Từ (1) và (2) => ABC = EDC (đpcm)
c) Gọi giao điểm của AE và BD là H
Xét Δ ABH và Δ EBH có:
AB = BE (gt)
ABH = EBH (câu a)
BH là cạnh chung
Do đó, Δ ABH = Δ EBH (c.g.c)
=> BHA = BHE (2 góc tương ứng)
Mà BHA + BHE = 180o (kề bù) nên BHA = BHE = 90o
=> BH⊥AEBH⊥AE hay BD⊥AE(đpcm)

\(\text{#TNam}\)
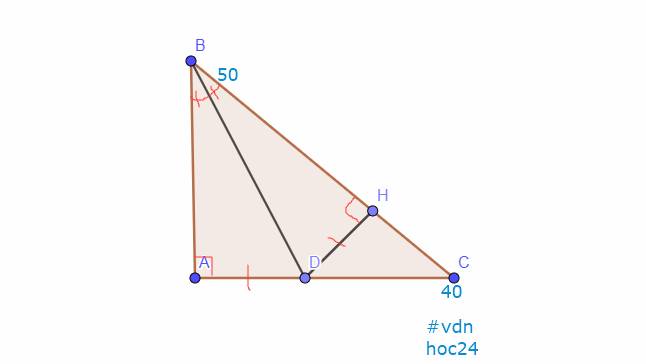
`a,` Ta có: \(\widehat{A}=90^0, \widehat{B}=50^0\)
Theo đlí tổng `3` góc trong `1` tam giác ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
`->`\(90^0+50^0+\widehat{C}=180^0\)
`->`\(\widehat{C}=180^0-90^0-50^0=40^0\)
`->`\(\widehat{A}>\widehat{B}>\widehat{C}\)
`-> BC>AC>AB`
`b,` Xét Tam giác `ABD` và Tam giác `HBD` có:
`\text {BD chung}`
\(\widehat{ABD}=\widehat{HBD}\) `(\text {tia phân giác}`\(\widehat{BAC})\)
`=> \text {Tam giác ABD = Tam giác HBD (ch-gn)}`
`-> AD = HD (\text {2 cạnh tương ứng})`
`c,` Xét Tam giác `HDC:`\(\widehat{H}=90^0\)
`-> \text {DC là cạnh lớn nhất}`
`-> DC>HD`
Mà `DA=DH (b)`
`-> DC>DA (đpcm)`

a. Tính góc ADB và góc BDC: Gọi góc ADB = x, góc BDC = y. Ta có thể sử dụng các quy tắc góc chắn cung và góc nội tiếp để tính góc như sau:
- Góc BAC = 90 độ (do tam giác ABC vuông tại A)
- Góc B = 60 độ (theo đề bài)
- Góc ABC = 180 - Góc BAC - Góc B = 30 độ (tổng các góc của tam giác ABC bằng 180 độ)
- Góc ABD = Góc ABC (do AB // CD theo định lý Thales)
- Góc DAB = 180 - Góc ADB - Góc ABD = 180 - x - 30
- Góc BCD = Góc BAC (do CD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDC)
- Góc BDC = 180 - Góc BCD - Góc B = 90 - Góc BAC/2 = 45 độ (do tam giác BCD cân tại B)
b. So sánh các cạnh của tam giác ABD: Để so sánh các cạnh của tam giác ABD, ta cần tính độ dài các cạnh. Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
- AB^2 = AC^2 + BC^2 = a^2 + b^2
- BC = a
- AC = b Vậy AB = sqrt(a^2 + b^2). Tương tự, ta có CD = b và BD = c*sqrt(3)/2 (tính theo phương pháp trong câu trả lời trước). Do đó, ta có thể so sánh các cạnh của tam giác ABD theo thứ tự tăng dần: CD < AB < BD.
c. So sánh các góc của tam giác BDC: Trong tam giác BDC, ta đã tính được góc BDC = 45 độ (như ở câu a). Do tam giác BDC cân tại B, nên góc CBD cũng bằng 45 độ. Vì vậy, hai góc của tam giác BDC bằng nhau và bằng 45 độ.
a. Tính góc ADB và góc BDC: Gọi góc ADB = x, góc BDC = y. Ta có thể sử dụng các quy tắc góc chắn cung và góc nội tiếp để tính góc như sau:
- Góc BAC = 90 độ (do tam giác ABC vuông tại A)
- Góc B = 60 độ (theo đề bài)
- Góc ABC = 180 - Góc BAC - Góc B = 30 độ (tổng các góc của tam giác ABC bằng 180 độ)
- Góc ABD = Góc ABC (do AB // CD theo định lý Thales)
- Góc DAB = 180 - Góc ADB - Góc ABD = 180 - x - 30
- Góc BCD = Góc BAC (do CD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDC)
- Góc BDC = 180 - Góc BCD - Góc B = 90 - Góc BAC/2 = 45 độ (do tam giác BCD cân tại B)
b. So sánh các cạnh của tam giác ABD: Để so sánh các cạnh của tam giác ABD, ta cần tính độ dài các cạnh. Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
- AB^2 = AC^2 + BC^2 = a^2 + b^2
- BC = a
- AC = b Vậy AB = sqrt(a^2 + b^2). Tương tự, ta có CD = b và BD = c*sqrt(3)/2 (tính theo phương pháp trong câu trả lời trước). Do đó, ta có thể so sánh các cạnh của tam giác ABD theo thứ tự tăng dần: CD < AB < BD.
c. So sánh các góc của tam giác BDC: Trong tam giác BDC, ta đã tính được góc BDC = 45 độ (như ở câu a). Do tam giác BDC cân tại B, nên góc CBD cũng bằng 45 độ. Vì vậy, hai góc của tam giác BDC bằng nhau và bằng 45 độ.

Bài 3:
a: Xét ΔAFC vuôngtại F và ΔAED vuông tại E có
AC=AD
góc FAC=góc EAD
=>ΔAFC=ΔAED
=>AF=AE
=>A là trung điểm cua EF
b: DE vuông góc AB
CF vuông góc AB
=>DE//CF
c: Xét tứ giác CFDE có
CF//DE
CF=DE
=>CFDE là hình bình hành
=>CE//DF

a: góc BAC=180-120=60 độ
góc ABE=70/2=35 độ
góc AEB=180-60-35=85 độ
b: góc ABE<góc BAE<góc AEB
=>AE<BE<AB
c: góc ECB=180-70-60=50 độ
góc BEC=180-85=95 độ
Vì góc EBC<góc ECB<góc BEC
nên EC<EB<BC

a) AC>BC>AB
b) BD<DC
giải chi tiết giùm mình nha