Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
A+B+C=180(tính chất của một tam giác)
⇒A=180-B-C
⇒A=180-20
⇒A=160
vì tia phân giác của góc A cắt BC tại D nên A1=A2=\(\dfrac{160}{2}\)=80
\(\Leftrightarrow\)D1=80
Vì góc D1 và góc D2 là 2 góc kề bù nên D1+D2=180
mà góc D1=80
\(\Rightarrow\)D2=180-80
\(\Rightarrow\)D2=100
Vay : D1=80, D2=100
mk ko viết đc kí hiệu góc và độ mong mọi người thông cảm![]()

\(\widehat{BAC}\)= 1800 - (\(\widehat{B}+\widehat{C}\)) = 1800 - ( 800 + 300)= 700
\(\widehat{A}_1\)=\(\widehat{A}_2\)=\(\dfrac{\widehat{A}}{2}\)=\(\dfrac{70^0}{2}\)= 350
\(\widehat{ADC}=\widehat{B}+\widehat{A}_1\)(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó \(\widehat{ADB}\)= 1800 - \(\widehat{ADC}\)= 1800 + 1150=650
Hình vẽ: 

Gọi A1, A2 là 2 góc được tạo ra bởi tia phân giác góc A.
Ta có:
Góc ∠BAC = 1800 – ( ∠B + ∠C)
= 1800 – ( 800 + 300) = 700
Hay ta có thể gọi ∠A = 700
Góc ∠A1 = ∠A2
= ∠A/2 = 700 /2 = 350
- Xét tam giác ADC ta có: Góc ∠ADC = 1800 – (∠C + ∠A2)
= 1800 – (350 + 300)= 1150
- Do đó góc ∠ADB = 1800 – ∠ADC
= 1800 – 1150
= 650

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: a=40; b=60; c=80

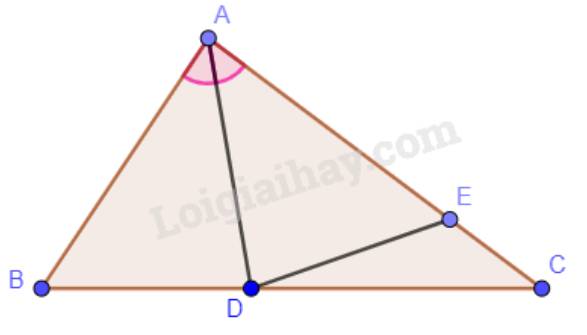
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).

-Do Ad là tia phân gaisc của \(\widehat{A}\) nên \(\widehat{BAD}\)\(=\widehat{CAD}\)= \(45^o\)
=> \(\widehat{BAH}\)\(=\widehat{BAD}-\widehat{HAD}=45^o-15^o=30^o\)
-Xét tam giác ABH vuông tại H có: \(\widehat{B}=90^o-\widehat{BAH}=90^o-30^o=65^o\)
-Xét tam giác ABC vuông tại A có: \(\widehat{C}=90^o-\widehat{B}=90^o-65^o=25^o\)
Vậy \(\widehat{B}=65^o\), \(\widehat{C}=25^o\)
