Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

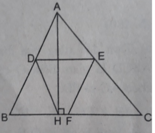
DECH là hình thang (vì có DE // CH);
BDEF là hình bình hành (vì có DE // BF và DE = BF)
DEFH là hình thang cân (vì có DE // HF và DF = HE = 1/2AC)

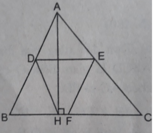
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2

a/ Xét t/g ABC có D,E lần lượt là trung điểm AB ; AC
=> DE là đường trung bình t/g ABC
=> DE // BC ; DE = BC/2
=> DE // BF ; DE = BF(do F là trung điểm BC)
=> Tứ giác BDEF là hình bình hành
b/ Có BDEF là hbh
=> EF = BD
Xét t/g ABK vuông tại K có KD là đường trung tuyến
=> KD = 1/2 AB = BD=> EF = KD
Mà DE // BC
=> DE // KF
=> Tứ giác DEFK là htc
c/ Xét t/g AHC có ME là đường trung binh
=> ME = 1/2 HC ; ME // HC (1)
Xét t/g BHC có NF là đường trung bình
=> NF = 1/2 HC ; NF // HC (2)
(1) ; (2)
=> ME = NF ; ME // NF (3)
Xét t/g ABH có MN là đường trung bình
=> MN // AB ; MN = 1/2 ABMà
HC ⊥ AB
NF // HC=> MN ⊥ NF (4)(3) ; (4)
=> MNFE là hcn
=> NE = MF ; NE, MF cắt nhau tại trung điểm mỗi đoạn
CMTT ta có đpcm

a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC và DE=BC/2
=>DE//BF và DE=BF
=>BDEF là hình bình hành
b: Xét ΔBAC có BD/BA=BF/BC
nên DF//AC và DF=AC/2
=>DF=EK
Xét tứ giác DEFK cos
DE//FK
DF=EK
Do đó: DEFK là hình thang cân

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
Xét ΔABH có
M là trung điểm của AB
MI//BH
Do đó: I là trung điểm của AH