Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

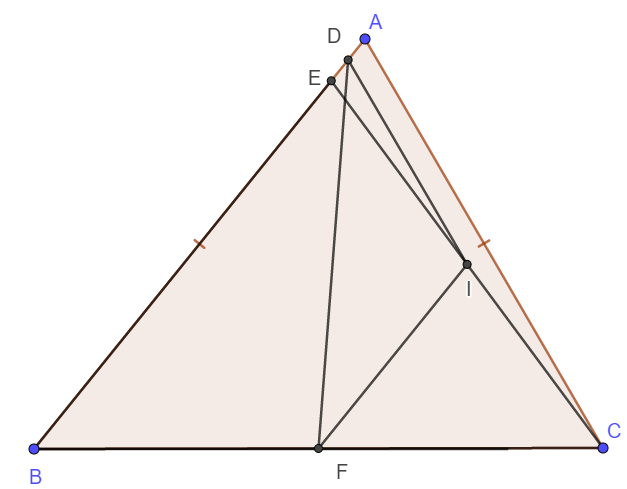
a) Xét tam giác ECB có I, F lần lượt là trung điểm của CE và CB nên IF là đường trung bình tam giác.
Suy ra \(IF=\frac{ED}{2}\)
Xét tam giác ECA có I, D lần lượt là trung điểm của CE và EA nên ID là đường trung bình tam giác.
Suy ra \(ID=\frac{AC}{2}\)
Mà AC = BE nên ID = IF
Vậy tam giác DIF cân tại I.
b) Do tam giác DIF cân tại I nên \(\widehat{FDI}=\widehat{DFI}\)
Lại có IF là đường trung bình tam giác BEC nên IF // AB, suy ra \(\widehat{DFI}=\widehat{FDB}\)
Từ đó ta có: \(\widehat{FDI}=\widehat{FDB}\Rightarrow\widehat{BDI}=2\widehat{IDF}\)
Cũng do DI là đường trung bình nên DI // AC hay \(\widehat{BDI}=\widehat{BAC}\)
Vậy nên \(\widehat{BAC}=2\widehat{IDF}\)

A B C M N D I
Nối C với D. Gọi I là trung điểm CD. Nối I với M và N.
Xét \(\Delta\)CAD: M là trung điểm AD; I là trung điểm CD => IM là đường trung bình của \(\Delta\)CAD
=> IM = AC/2 (1)
Tương tự: IN là đường trung bình của \(\Delta\)CBD => IN = DB/2 (2)
Từ (1) và (2) => IM =IN => \(\Delta\)MIN cân ở I => ^IMN = ^INM.
Lại có: IN là đường trung bình \(\Delta\)CBD => IN // BD hay IN // BM => ^INM = ^BMN (So le trg)
=> ^IMN = ^BMN = 1/2 ^BMI.
Mặt khác: IM là đường trung bình \(\Delta\)CAD => IM // AC => ^BMI = ^BAC (Đồng vị)
=> ^BMN = 1/2. ^BAC hay ^BAC = 2.^BMN (đpcm).

Bài 2:
a: Xét hình thang ABCD có
N là trung điểm của AD
M là trung điểm của BC
Do đó: NM là đường trung bình
=>NM//AB//CD
=>NM\(\perp\)AD
Xét ΔMAD có
MN là đường cao
MN là đường trung tuyến
Do đó: ΔMAD cân tại M
b: Ta có: \(\widehat{MAB}+\widehat{MAD}=90^0\)
\(\widehat{MDC}+\widehat{MDA}=90^0\)
mà \(\widehat{MAD}=\widehat{MDA}\)
nên \(\widehat{MAB}=\widehat{MDC}\)