Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

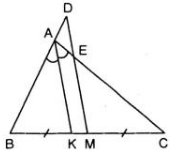
AK là đường phân giác của tam giác ABC nên:
Ta có: MD // AK
⇒ ΔABK  ΔDBM và ΔECM
ΔDBM và ΔECM 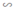 ΔACK
ΔACK
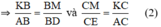
Từ (1) và (2) ta có: 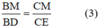
Do BM = CM (giả thiết) nên từ (3) suy ra: BD = CE.

Bài 1:
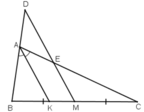
Xét tam giác $BDM$ có $AK\parallel DM$, áp dụng đl Talet:
$\frac{BA}{BD}=\frac{BK}{BM}=\frac{2BK}{BC}(*)$
Xét tam giác $CAK$ có $ME\parallel AK$, áp dụng đl Talet:
$\frac{CE}{CA}=\frac{CM}{CK}=\frac{BC}{2CK}(**)$
Lấy $(*)$ nhân $(**)$ thì:
$\frac{CE}{BD}.\frac{AB}{AC}=\frac{BK}{CK}$
Mà: $\frac{BK}{CK}=\frac{AB}{AC}$ (theo tính chất tia phân giác)
$\Rightarrow \frac{CE}{BD}=1$
$\Rightarrow CE=BD$ (đpcm)

Qua K vẽ đường thẳng // với AB cắt AC tại H.
=> AHKD là hình bình hành => DK = AH (1)
Gọi giao điểm của AK và DH là O. Vì AHKD là HBH => DO = OH
Xét 3 đường thẳng MA, CA, BA đồng quy tại A cắt 2 đường thẳng DH và BC ta được: DO/OH = BM/MC = 1
=> DH // BC (định lí chùm đường thẳng đồng quy đảo)
Xét ∆ ADH và ∆ FEC có:
AD = EF ( t/c đoạn chắn) ; DH = EC (t/c đoạn chắn) ; ^ADH = ^FEC => ∆ ADH = ∆ FEC (c-g-c)
=> AH = CF (2)
Từ (1) và (2) => CF = DK (đpcm)
GL
Do EF//AB⇒\(\frac{CF}{CA}=\frac{EF}{AB}\)⇒\(\frac{CF}{EF}=\frac{AC}{AB}\)(1)
Dựng MG//AC và MM là trung điểm cạnh BC
⇒GM là đường trung bình ΔABC
=⇒G là trung điểm cạnh AB ⇒AG=BG
Do DK//GM⇒\(\frac{AD}{AG}=\frac{DK}{GM}\)⇒\(\frac{AD}{BG}=\frac{DK}{GM}\)
=> \(\frac{DK}{AD}=\frac{GM}{BG}=\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB}\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\frac{CF}{EF}=\frac{DK}{AD}\)
Mà tứ giác ADEF là hình bình hành (vì EF//AD và DE//AF) nên AD=EF
=> CF=DK (đpcm)
Nguồn: thuynga

Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )

a: Xét ΔBNQ có
C là trung điểm của BQ
CA//NQ
Do đó: A là trung điểm của NB
Xét ΔCPM có
B là trung điểm của CP
CA//MP
DO đó: A là trung điểm của CM
Xét tứ giác BMNC có
A là trung điểm chung của BN và MC
nên BMNC là hình bình hành
b: Để ANKM là hình bình hành
nên AM//KN và AN//KM
=>AB//MK và AB=MK
=>ABMK là hình bình hành
=>AI//BM
Xét ΔCBM có
A là trung điểm của CA
AI//BM
DO đó; I là trung điểm của BC