Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b,
d là đường trung trực của BC (gt) ⇒ d ⊥ BC
A và K đối xứng qua d nên d lả trung trực của AK ⇒ d ⊥ AK
Suy ra: BC //AK. Tứ giác ABCK là hình thang.
AC và KB đối xứng qua d nên AC = BK
Vậy hình thang ABCK là hình thang cân.
Chúc bạn học tốt !!!

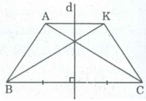
d là đường thẳng trung trực của BC nên B và C đối xứng qua d
K đối xứng với A qua d
Nên đoạn thẳng đối xứng với đoạn AB qua d là đoạn KC
Đoạn thẳng đối xứng với đoạn AC qua d là đoạn KB.

a. MN = ?
Trong ΔABC có:
M là trung điểm AB (gt)
N là trung điểm AC (gt)
⇒ MN là đường trung bình ΔABC
⇒ MN = 1/2BC (t/c)
Mà BC = 6cm (gt)
⇒ MN=BC/2=6/2=3(cm)
b. C/m: BMNC là hình thang cân
Có MN là đường trung bình ΔABC
⇒ MN//BC
⇒ BMNC là hình thang
Mà góc ABC = góc ACB (ΔABC cân tại A)
⇒ BMNC là hình thang cân (DHNB)
c. C/m: ABCK là hình bình hành
Xét tứ giác ABCK có:
N là trung điểm AC (gt)
N là trung điểm BK (K đ/x với B qua M)
⇒ ABCK là hình bình hành (DHNB)
d. C/m: AHBP là hình chữ nhật
Xét tứ giác AHBP có:
M là trung điểm AB (gt)
M là trung điểm PH ( H đ/x với P qua M)
⇒ AHBP là hình bình hành (DHNB)
Có ΔABC cân tại A
⇒ AP là trung tuyến đồng thời là đg cao
⇒ góc APB = 90 độ
⇒ AHBP là hình chữ nhật (DHNB)

a) Giao điểm của AH và BC là E. Dễ thấy: \(\Delta\)BHM = \(\Delta\)CKM (c.g.c) => ^HBM = ^KCM
=> ^HBC = ^KCB. Do H đối xứng với I qua BC => ^HBC = ^IBC => ^KCB = ^IBC (1)
Xét \(\Delta\)HIK: E là trung điểm IH; M là trung điểm của HK => EK là đường trung bình \(\Delta\)HIK
=> EM // IK hay IK // BC => Tứ giác BIKC là hình thang (2)
Từ (1) & (2) => Tứ giác BIKC là hình thang cân (đpcm).
b) Dễ c/m tứ giác BHCK là hình bình hành (Do có tâm đối xứng) => HC // BK
Hay HC // GK => Tứ giác GHCK là hình thang
Để tứ giác GHCK là hình thang cân thì ^GHC = ^KCH
<=> ^HAC + ^HCA = ^HCB + ^HBC <=> ^HCA = ^HCB ( Vì ^HAC = ^HBC, cùng phụ ^ACB)
<=> CH là phân giác ^ACB. Mà CH cũng là đường cao của \(\Delta\)ABC => \(\Delta\)ABC cân tại C
Vậy khi \(\Delta\)ABC cân tại C thì tứ giác GHCK là hình thang cân.

a,Kẻ tam giác ABC sau đó nối C với K,B với K sẽ nhìn thấy đoạn thẳng đối xứng với AB và AC qua d.

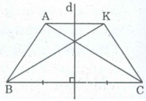
d là đường trung trực của BC (gt) ⇒ d ⊥ BC
A và K đối xứng qua d nên d lả trung trực của AK ⇒ d ⊥ AK
Suy ra: BC //AK. Tứ giác ABCK là hình thang.
AC và KB đối xứng qua d nên AC = BK
Vậy hình thang ABCK là hình thang cân.