Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)`
Có `Delta ABC` cân tại `A(g t)`
`=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
Xét `Delta BEC` và `Delta CDB` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(BC-chung),(hat(EBC)=hat(DCB)(cmt)):}}`
`=>Delta BEC=Delta CDB(c.h-g.n)`
`=>CE=BD` ( 2 cạnh tương ứng )( dpcm )
`b)`
Có `Delta BEC=Delta CDB(cmt)`
`=>hat(C_1)=hat(B_1)` ( 2 góc tương ứng )
`=>Delta BOC` cân tại `O`
`=>OB=OC`(dpcm)
Xét `Delta OEB` và `Delta ODC` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(OB=OC(cmt)),(hat(O_1)=hat(O_2)(doi.di nh)):}}`
`=>Delta OEB=Delta ODC(c.h-g.n)`
`=>OE=OD`( 2 cạnh tương ứng )(dpcm)
`c)`
Có `Delta ABC` cân tại `A(g t)`
`=>AB=AC`
`=>A in ` trung trực của `Delta ABC(1)`
Có `OB=OC(cmt)`
`=>O in` trung trực của `Delta ABC(2)`
Từ `(1)` và `(2)=>OA` là trung trực `Delta ABC`
mà `Delta ABC` cân tại `A`
Nên `OA` là phân giác `hat(BAC)` (dpcm)
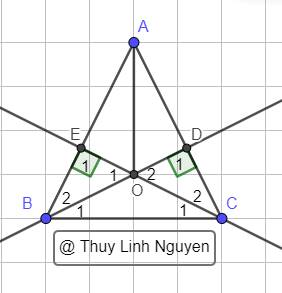

a) t/g ABC cân tại A
=> ABC = ACB ( tính chất tam giác cân)
Xét t/g DCB vuông tại D và tam giác EBC vuông tại E có:
BC là cạnh chung
DCB = EBC (cmt)
Do đó, t/g DCB = t/g EBC ( cạnh huyền - góc nhọn)
=> BD = CE (2 cạnh tương ứng) (đpcm)
b) t/g DCB = t/g EBC (câu a)
=> CD = BE (2 cạnh tương ứng)
DBC = ECB (2 góc tương ứng)
Mà ABC = ACB (câu a)
=> ABC - DBC = ACB - ECB
=> ABD = ACE
Xét t/g EBO vuông tại E và t/g DCO vuông tại D có:
BE = CD (cmt)
EBO = DCO (cmt)
Do đó, t/g EBO = t/g DCO ( cạnh góc vuông và góc nhọn kề)
=> OB = OC (2 cạnh tương ứng) (1)
OE = OD (2 cạnh tương ứng) (2)
Từ (1) và (2) => đpcm
c) Dễ thấy, t/g AOC = t/g AOB (c.c.c)
=> OAC = OAB (2 góc tương ứng)
=> AO là phân giác CAB (đpcm)
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có:
AB = AC (gt)
Góc A chung
=> ΔABD = ΔACE ( cạnh huyền - góc nhọn )
=> BD = CE ( 2 cạnh tương ứng )
b) Vì ΔABD = ΔACE nên góc ABD = ACE ( 2 góc tương ứng ) và AD = AE ( 2 cạnh tương ứng )
Ta có: AD + DC = AC
AE + EB = AB
mà AD = AE (cm trên); AC = AB (gt)
=> DC = EB
Xét ΔEOB và ΔDOC có:
góc ABD = ACE (cm trên)
EB = DC (cm trên)
góc OEB = ODC (= 90)
=> ΔEOB = ΔDOC (g.c.g)
=> OE = OD ( 2 cạnh tương ứng ) ; OB = OC ( 2 cạnh tương ứng )
c) Do ΔEOB = ΔĐỌC nên EO = DO ( 2 cạnh tương ứng )
Xét ΔAOE vuông tại E và ΔAOD vuông tại D có:
OE = DO ( cm trên )
AE = AD (câu b)
=> ΔAOE = ΔAOD ( cạnh góc vuông )
=> góc OAE = OAD ( 2 góc tương ứng )
Do đó AO là tia phân giác của góc EAD hay AO là tia pg của góc BAC.
Chúc học tốt Cathy Trang

Xét \(\Delta BEC\) và \(\Delta CDB\) có :
\(\widehat{BEC}=\widehat{CDB}=90^o\left(gt\right)\)
BC : cạnh chung
\(\widehat{B}=\widehat{C}\) ( vì \(\Delta ABC\) có AB = AC \(\Rightarrow\) \(\Delta ABC\) cân tại A )
\(\Rightarrow\Delta BEC=\Delta CDB\)(cạnh huyền - góc nhọn )
\(\Rightarrow BD=CE\)
b ) Vì \(\Delta BEC=\Delta CDB\left(cmt\right)\)
\(\Rightarrow BE=CD\)
Có : \(AB=AE+BE\)
\(AC=AD+DC\)
Mà AB = AC (gt) ; BE = CD (cmt)
\(\Rightarrow AE=AD\)
Xét \(\Delta AOE\) và \(\Delta AOD\) có :
\(AE=AD\left(cmt\right)\)
\(\widehat{AEO}=\widehat{ADO}=90^o\left(gt\right)\)
OA : cạnh chung
\(\Rightarrow\Delta AOE=\Delta AOD\) ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow OE==OD\)
c ) Vì \(\Delta BEC=\Delta CDB\) (cmt)
\(\Rightarrow\widehat{BCE}=\widehat{CBD}\)
\(\Rightarrow\Delta AOB\) cân tại O
\(\Rightarrow OB=OC\)
d ) Vì \(\Delta AOE=\Delta AOD\left(cmt\right)\)
\(\Rightarrow\widehat{OAE}=\widehat{OAD}\)
\(\Rightarrow AO\) là tia phân giác của góc BAC
Chúc bạn học tốt !!!

a)tam giác BDA = tam giác CEA (CH -GN)
=> BD =CE
b)tam giác ADO = tam giác AEO (CH - GN)
=> OD = OE
ta có : BD+OD = CE + OE
BD = CE; OD = OE; BD+OD=BO; CE+OE = CO
=> BO=CO
c) ta có BE là đường cao của tam giác BOC; CD là đường cao của tam giác BOC
=> OA là đường cao thứ 3
tam giác BOC cân tại O có đường cao cũng là đường phân giác nên OA là đường phân giác của góc BAC

a) Xét tam giác ABD và tam giác ACE có
góc ADB = góc AEC = 90 độ
AB=AC
góc A: chung
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn)
=> BD=CE và AD=AE
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD
Xét tam giác OEB và tam giác ODC có
góc OEB = góc ODC = 90 độ
BE=CD
góc BOE = góc COD (đối đỉnh)
=> tam giác OEB = tam giác ODC => OB=OC
c) Xét tam giác AOB và tam giác AOC có
AB=AC
OB=OC
AO: cạnh chung
=> tam giác AOB = tam giác AOC (c.c.c)
=> góc OAB=góc OAC
=> AO la tia phân giác góc BAC
Bài mk lm như dzị ak
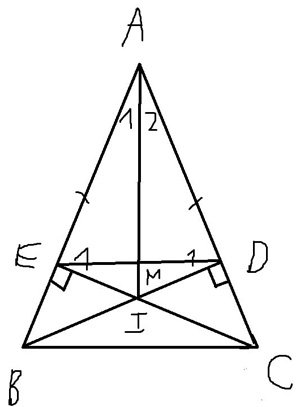 a, tg ADB và tg AEC có
a, tg ADB và tg AEC có^E1 = ^D1 = 90 độ
AB = AC
^A chung
=> tg ADB = tg AEC
=> AD = AE
=> tg ADE cân
b, tg ABI và tg ACI có
^E1 = ^D1 = 90 độ
AI chung
AB = AC
=> tg ABI = tg ACI
=> ^A1 = ^A2 ( góc t/ứ)
=> IB = IC ( cạnh t/ứ)
=> tg IBC cân
c, vì ^A1 = ^A2 ( câu b )
=> AI là tpg của góc EAD