Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) cm dễ
b) Tứ giác BCEF có góc BEC = góc BFC = 900 nên nội tiếp
Xét tam giác AEF và tam giác ABC có : góc A chung, góc AEF = góc ABC (BCEF nội tiếp) nên đồng dạng
c) Kẻ đường kính AM của (O)
góc ABM = 900 (góc nội tiếp chắn nửa (O)) => AB vuông góc BM mà AB vuông góc CH => BM // CH
cmtt ta cũng có CM // BH. Vậy tứ giác BHCM là hình bình hành
mà N là trung điểm của BC => N là trung điểm của HM => ON là đường tb của tam giác AHM => ON = 1/2AH hay AH = 2ON

a: góc BEH+góc BFH=90 độ
=>BEHF nội tiếp
b: góc ABK=1/2*sđ cung AK=90 độ
Xét ΔABK vuông tại B và ΔAFC vuông tại F có
góc AKB=góc ACF
=>ΔABK đồng dạng với ΔAFC

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
b; góc ACK=1/2*sđ cung AK=90 độ
Xét ΔACK vuông tại C và ΔADB vuông tại D có
góc AKC=góc ABD
=>ΔACK đồng dạng với ΔADB
=>AC/AD=AK/AB
=>AC*AB=AD*AK

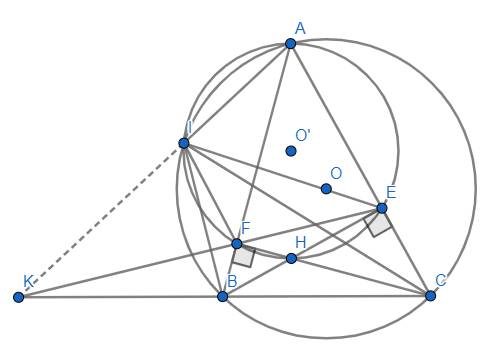
(a) Gọi \(O'\) là tâm đường tròn ngoại tiếp tứ giác \(AIFE.\)
Ta có : \(\hat{IEF}=\hat{IAF}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{IEF}=\hat{IAB}.\)
Mà : \(\hat{IAB}=\hat{ICB}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(IB\)).
Do đó, \(\hat{IEF}=\hat{ICB}.\)
Ta cũng có : \(\hat{FIE}=\hat{FAE}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{FIE}=\hat{BAC}.\)
Mà : \(\hat{BAC}=\hat{BIC}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(BC\)).
Do đó, \(\hat{FIE}=\hat{BIC}.\)
Xét \(\Delta IBC,\Delta IFE:\left\{{}\begin{matrix}\hat{ICB}=\hat{IEF}\left(cmt\right)\\\hat{BIC}=\hat{FIE}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta IBE\sim\Delta IFE\left(g.g\right)\) (đpcm).
(b) Mình tạm thời chưa nghĩ ra nhé:)

1: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
2: Gọi Ax là tiếp tuyến tại A của (O)
góc xAC=1/2*sđ cung AC
góc ABC=1/2*sđ cung AC
=>góc xAC=góc ABC
mà góc ABC=góc AEF
nên góc AEF=góc xAC
=>EF//Ax
=>OA vuông góc EF


trả lời
đề này bn làm đc câu mấy rồi
hok tốt
khong giỏi hình, mk chỉ cần câu c