Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.

a: Gọi H là trung điểm của BC
Xét ΔABC có AH là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AH}\)
ΔABC đều có AH là đường trung tuyến
nên \(AH=AB\cdot\dfrac{\sqrt{3}}{2}=3a\cdot\dfrac{\sqrt{3}}{2}\)
=>\(2\cdot AH=3a\sqrt{3}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AH=3a\sqrt{3}\)
b:
Gọi I là trung điểm của AH
I là trung điểm của AH
=>\(IA=IH=\dfrac{3a\sqrt{3}}{2}\)
ΔABC đều
mà AH là đường trung tuyến
nên AH vuông góc BC
ΔIHC vuông tại H
=>\(CI^2=HI^2+HC^2\)
=>\(CI^2=\left(\dfrac{3a\sqrt{3}}{2}\right)^2+\left(1,5a\right)^2=9a^2\)
=>CI=3a
\(\left|\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(=\left|2\cdot\overrightarrow{CI}\right|=2CI\)
\(=2\cdot3a=6a\)

Bài 3:
\(\text{Δ}=1^2-4\cdot2\cdot\left(-4m-2\right)\)
=1+8(4m-2)
=32m-16+1=32m-15
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>32m-15>0
hay m>15/32
Để phương trình vô nghiệm thì 32m-15<0
hay m<15/32
Để phương trình có nghiệm kép thì 32m-15=0
hay m=15/32

a: ABCD là hình vuông
=>AC là phân giác của góc BAD và \(AC^2=AB^2+BC^2\)
AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}=\dfrac{1}{2}\cdot90^0=45^0\)
\(AC^2=AB^2+BC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB};\overrightarrow{AC}\right)\)
\(=a\cdot a\sqrt{2}\cdot cosBAC\)
\(=a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)
b: Vì ABCD là hình vuông
nên AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)

\(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}\left(\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BA}+\overrightarrow{AB}.\overrightarrow{AD}\)
\(=0-\overrightarrow{AB}^2+0=-4a^2\)

Tham khảo:
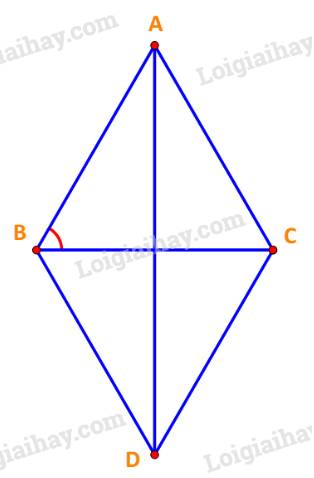
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.
\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).