Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

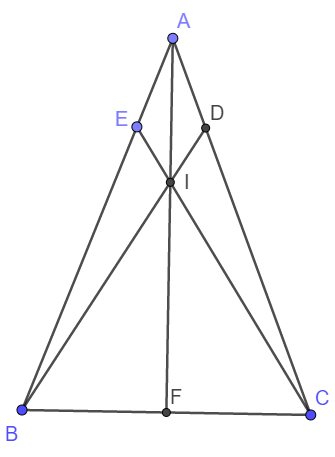
a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath
Bài này easy lắm bạn
a) Xét \(\Delta\) ABD và \(\Delta\)ACE có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AD = AE ( gt)
=> \(\Delta\)ABD = \(\Delta\) ACE (c-g-c)
=> BD = CE ( 2 cạnh tương ứng )
+) Ta có \(\hept{\begin{cases}AB=AC\left(gt\right)\\AE=AD\left(cmt\right)\end{cases}}\)
\(\Rightarrow AB-AE=AC-AD\)
\(\Rightarrow\)BE = CD
+) Xét \(\Delta\)CEB và \(\Delta\)BDC có
CE = BD ( cmt)
EB = DC ( cmt)
CB: cạnh chung
=> \(\Delta\)CEB = \(\Delta\) BDC (c-c-c)
2 câu này đã nhé