Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Vì tứ giác ABCD là hình thang AB//CD nên góc A+ góc D=180 độ mà góc A- góc D=40 do suy ra goc D= (180-40):2=70 do suy ra goc A= 180-70=110 do
Tương tự ta cũng có: \(\widehat{B}+\widehat{C}=180^0\)ma \(\widehat{B}=4\times\widehat{C}\)\(\Rightarrow4\times\widehat{C}+\widehat{C}=180^0\Rightarrow5\times\widehat{C}=180^0\Rightarrow\widehat{C}=36^0\Rightarrow\widehat{B}=180^0-36^0=144^0\)
Còn bài 2 thì tớ chưa nghĩ ra bạn rang đoi nhá
2. Vì AB//DC ma \(K\in AB\Rightarrow\widehat{AKD}=\widehat{KDC};\widehat{BKC}=\widehat{KCD}\) (1)
Vì DK là tia phân giác của \(\widehat{ADC}\Rightarrow\widehat{ADK}=\widehat{KDC}\)và CK là tia phân giác của \(\widehat{BCD}\Rightarrow\widehat{KCB}=\widehat{KCD}\)(2)
Từ(1) vả (2) ta có: \(\widehat{AKD}=\widehat{ADK};\widehat{BKC}=\widehat{BCK}\)suy ra tam giác AKD cân tại A và tam giác KBC cân tại B
\(\Rightarrow AK=AD;BK=BC\Rightarrow AK+BK=AD+BC\Rightarrow AB=AD+BC\)

A B C D
a) Vì AB = AC = BC (△ABC đều)
Mà AB = BD \(\Rightarrow\)BD = BC \(\Rightarrow\)△BDC cân tại B
Khi đó ta có: \(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{ACB}\\\widehat{BDC}=\widehat{BCD}\end{matrix}\right.\)
Xét △ADC có: BAC + BDC + DCA = 180o (định lí tổng ba góc △)
\(\Rightarrow\)BAC + BDC + BCD + BCA = 180o
\(\Rightarrow\)2(BCD + BCA) = 180o
\(\Rightarrow\)ACD = 90o
\(\Rightarrow\)DC \(\perp\)AC (đpcm)
b) Vì AB = 3 cm
\(\Rightarrow\) \(\left\{{}\begin{matrix}AC=3cm\\AD=3.2=6cm\end{matrix}\right.\)
Xét △ACD vuông tại C
\(\Rightarrow CA^2+CD^2=AD^2\) (định lí Pytago)
\(\Rightarrow CD=\sqrt{AD^2-CA^2}=\sqrt{6^2-3^2}=\sqrt{27}cm\)

a) Xét ΔBED và ΔBEC có
BD=BC(gt)
\(\widehat{DBE}=\widehat{CBE}\)(BE là tia phân giác của \(\widehat{DBC}\))
BE chung
Do đó: ΔBED=ΔBEC(c-g-c)
Xét ΔBDI và ΔBCI có
BD=BC(gt)
\(\widehat{DBI}=\widehat{CBI}\)(BI là tia phân giác của \(\widehat{DBC}\))
BI chung
Do đó: ΔBDI=ΔBCI(c-g-c)
⇒ID=IC(hai cạnh tương ứng)
b) Sửa đề: Chứng minh AH//BI
Xét ΔBDC có BD=BC(gt)
nên ΔBDC cân tại B(Định nghĩa tam giác cân)
Ta có: ΔBDC cân tại B(cmt)
mà BI là đường phân giác ứng với cạnh đáy DC(gt)
nên BI là đường cao ứng với cạnh DC(Định lí tam giác cân)
⇒BI⊥DC
Ta có: AH⊥DC(gt)
BI⊥DC(cmt)
Do đó: AH//BI(Định lí 1 từ vuông góc tới song song)


Vì a, b, c, d ≠ 0 nên ta có thể đặt 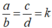 ⇒ a = kb; c = kd
⇒ a = kb; c = kd
Ta có:
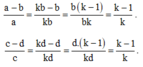
Suy ra 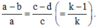
Cách 2:
Từ 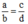 ta suy ra
ta suy ra 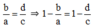 hay
hay